-
压力传感是石油勘探、军工监测和地震波信号采集等方面常用的一项压力测量技术,其传感器主要包括电学和光纤传感器。光纤传感器由于其结构小、灵敏度高和寿命长等优点已在许多方面代替电学传感器,但它在兵器工业、冶金工业、航空航天等高达几百兆帕的压力测量环境下,未有较高的形变量、压力灵敏度和抗干扰能力。为了解决传统光纤在压力作用下形变小和压力灵敏度低等问题,引入新型材料光子晶体光纤(photonic crystal fiber, PCF)。
1987年,YABLONOVITCH和JOHN[1-2]首次提出光子晶体的概念。2008年,YU等人[3]对压力作用下光子晶体光纤相关参量进行了分析,表明了光子晶体光纤可用作压力传感器中的敏感元件,帮助压力传感器的进一步发展。2011年,PARK等人[4]在PCF纤芯空气孔周围掺入了具有高折射率的GeO2,增大包层与纤芯之间的折射率差,减少限制损耗,提高了PCF结构的设计灵活度。2016年,YANG等人[5]采用固体偏压PCF,建立了基于双段偏振PCF Sagnac干涉仪的侧压传感系统,侧压力和温度分别进行测试,侧压灵敏度可达到0.2877nm/N,且温度变化引起的漂移小于0.1pm/℃。2017年,LÜ等人[6]采用双芯结构PCF作为光波导的横向应力传感器,建立了PCF结构的形变模型和表面等离子体共振效应耦合波模型,得到了横向应力与基模的共振峰位移之间的关系。同年,LIANG等人[7]提出了一种基于双芯光子晶体光纤的高灵敏度椭圆侧芯表面等离子体共振折射率传感模型。在该模型下,折射率和传感曲线线性度高。2018年,ZHANG等人[8]设计了一种以椭圆空气孔为纤芯,四周环绕正方形空气孔的光子晶体光纤结构。获得了光子晶体光纤的高双折射和色散平坦特性。PENG等人[9]提出一种基于大纤芯的单芯光子晶体光纤表面等离子体共振(surface plasmon resonance, SPR)传感结构实现了较高的传感灵敏度。同年,LIAO等人[10]设计了一种中心带有椭圆空气孔缺陷的光子晶体光纤,使光纤的双折射达到了10-2数量级。
作者参考以上PCF在理论和实验等方面取得的突破性研究,如设计特定结构实现高双折射、低损耗和大模场面积等特性,引入PCF作为传感单元,基于高双折射提出一种高灵敏度压力PCF传感器,通过高掺杂非对称性PCF结构,实现了更高的精度、敏感性和稳定性,获得更大的压力测量范围,可应用于上述压力场景,且单元尺寸小、空气孔为圆形,易于集成和工艺加工。
-
当PCF施加压力后,PCF横截面将会发生几何形变,产生各向异性的应力分布。同时,由于弹光效应的存在,将会改变原有的折射率,并改变相位模式双折射。
当PCF静态时,模式双折射为:
$ B_{0}=\left|n_{\mathrm{eff}, x}-n_{\mathrm{eff}, y}\right| $
(1) 式中,neff, x和neff, y为两个正交偏振模式的有效折射率,可由COMSOL仿真得到。
当PCF施加压力后,通过COMSOL可得到PCF横截面的应力分布和几何形变。此时,空气孔折射率不发生改变,SiO2折射率由下式决定:
$ \left\{\begin{array}{l}{n_{x}=n_{0}+C_{1} \sigma_{x}+C_{2}\left(\sigma_{y}+\sigma_{z}\right)} \\ {n_{y}=n_{0}+C_{1} \sigma_{y}+C_{2}\left(\sigma_{x}+\sigma_{z}\right)} \\ {n_{z}=n_{0}+C_{1} \sigma_{z}+C_{2}\left(\sigma_{x}+\sigma_{y}\right)}\end{array}\right. $
(2) 式中,弹光系数C1和C2与波长没有关系,C1=6.5×10-13m2/N,C2=4.2×10-12m2/N。聚碳酸脂[11]的弹性模量E=2.412GPa,泊松比ν=0.37,弹光系数C1=2.45×10-11m2/N,C2=9.38×10-11m2/N。
在COMSOL仿真时,通过(2)式将结构力学中的应力分布转化为PCF材料施加压力后的折射率输入到电磁波频域中,即可得到施加压力后两个正交偏振基模的有效折射率,再根据(1)式可得出施加压力后的相位模式双折射为:
$ B_{p}=\left|n_{\mathrm{eff}, x, p}-n_{\mathrm{eff}, y, p}\right| $
(3) 式中,neff, x, p和neff, y, p为施加压力后的两个正交偏振基模有效折射率。
通过静态时相位模式双折射B0和施加压力后得到的相位模式双折射Bp可得到相位模式双折射B。相位模式双折射灵敏度为:
$ \frac{\Delta B}{\Delta p}=\frac{B_{p}-B_{0}}{p} $
(4) 式中,p为外部施加的压力, ΔB表示双折射的变量,Δp表示压力变化量。可得到压力偏振相位灵敏度为:
$ K_{p}=\frac{2 \pi}{\lambda}\left(\frac{\Delta B}{\Delta p}+B l_{p}\right) $
(5) 式中,λ为曲空间波长,在测量横向压力时,压力诱导PCF的轴向伸长lp是很小的,且相位模式双折射B也很小,因此在计算(5)式中的第2项时,可以忽略轴向伸长lp对偏振相位灵敏度的影响,整理(5)式得:
$ K_{p}=\frac{2 {\rm{ \mathsf{ π} }}}{\lambda} \frac{\Delta B}{\Delta p} $
(6) -
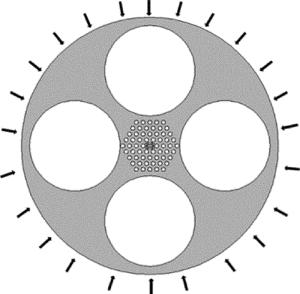
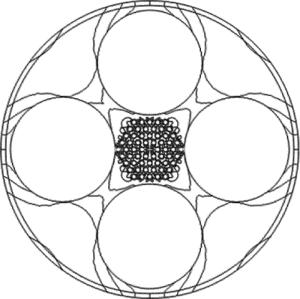
与普通双折射光纤相比,边孔型光纤[12-13]不仅具有较好的热稳定性,而且还具有较高的压力灵敏度,在压力传感时能较好的提升压力灵敏度并降低温度对传感性能的影响。聚碳酸酯作为芯区填充材料,具有较高的弹光系数,为压力敏感材料,同时其折射率(在1.55μm,20.4℃时)为1.586,高于SiO2的折射率,可以提高PCF的双折射率,在光波段有较好的透光性和较小的损耗[14]。基于以上特点,作者将边孔引入到高双折射PCF中并在纤芯掺入压力敏感材料有机材料聚碳酸酯,创新性的提出一种新型边孔型高双折射PCF,该结构综合了边孔型光纤和高双折射PCF的优点,具有较高的双折射,同时应用于压力传感时具有较高的压力灵敏度,且无需进行温度补偿。图 1为新型边孔型高双折射PCF横截面图。图 2为新型边孔型高双折射PCF横截面局部放大图。用石英(SiO2)作为背景材料,在包层空气孔中分别对称性的引入4个边孔大空气孔和周期性排列的小空气孔,近芯区上下左右各引入两个空气孔,使用聚碳酸酯填充椭圆形芯区。图 1中,D为PCF的直径,R为大空气孔的半径,d1为大空气孔圆心到纤芯中心的距离。图 2为图 1的局部放大图,d为包层周期性排列空气孔的直径,Λ为周期性排列空气孔的周期,d2和d3分别为芯区大空气孔和小空气孔的直径,X2, X3, Y2及Y3为近芯区空气孔圆心以芯区中心为原点的坐标绝对值,a和b分别为椭圆的长半轴和短半轴。
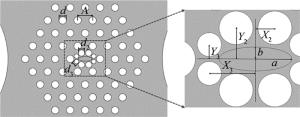
Figure 2. Partial enlarged drawing of cross-sectionof new structure of PCF with side hole and high birefringence
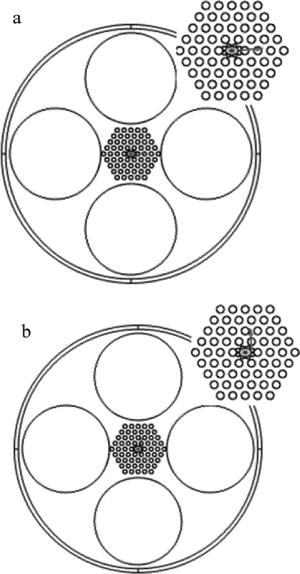
图 3为边孔型高双折射PCF施加静态液体压力分布图。静态液体压力是从PCF四周各个方向指向其中心。
-
利用COMSOL对图 3施加边界载荷,通过(2)式将施加压力后在PCF中产生的应力分布转化成PCF中的折射率分布,从而对COMSOL中的固体力学应力场与电磁波频域电场进行多物理场耦合,最终得出施加压力后的相位模式双折射。图 4为施加压力后的应力分布图。图 5为施加压力后的两个正交偏振基模。
-
p=200MPa时,不同长半轴a和短半轴b下的相位模式双折射灵敏度随长半轴a和短半轴b的变化如图 6所示。其中相位模式双折射灵敏度由(4)式求得。
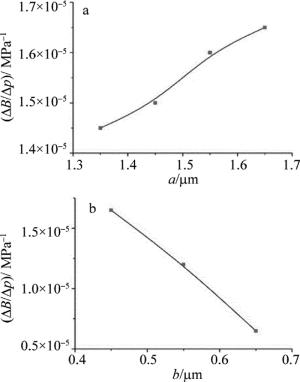
Figure 6. Relationship between phase mode birefringence sensitivity and different parameters a and b
随着所施加压力的增加,双折射也呈线性关系逐渐增加,增加幅度与改变的参量有关,长半轴a的影响大于短半轴b。由图 6可知,当a增加时,相位模式双折射灵敏度逐渐增加,而当b增加时,相位模式双折射灵敏度逐渐减小。
-
p=200MPa时,不同d2和d3下的相位模式双折射灵敏度随d2和d3的变化如图 7所示。
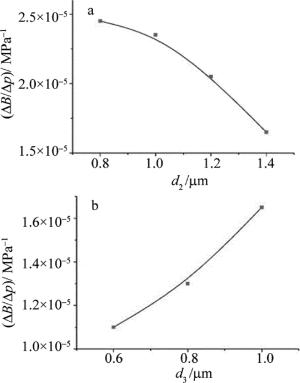
Figure 7. Relationship between phase mode birefringence sensitivity and different parameters d2 and d3
随着所施加压力的增加,双折射也呈线性关系逐渐增加,增加幅度与改变的参量有关,d2的影响大于d3。由图 7可知,当d3增加时,相位模式双折射灵敏度逐渐增加,而当d2增加时,相位模式双折射灵敏度逐渐减小。
-
p=200MPa时,不同d/Λ, Λ和空气孔层数N下的相位模式双折射灵敏度随三者的变化如图 8所示。

Figure 8. Relationship between phase mode birefringence sensitivity and different parameters d/Λ, Λ and N
随着所施加压力的增加,双折射呈线性关系逐渐增加,增加幅度与改变的参量有关,d/Λ, Λ和N对双折射有显著的影响。由图 8可知,当d/Λ和N增加时,相位模式双折射灵敏度逐渐增加,且d/Λ呈非线性关系; 当Λ增加时,相位模式双折射灵敏度逐渐减小。
-
p=200MPa时,不同R和d1下的相位模式双折射灵敏度随R和d1的变化如图 9所示。
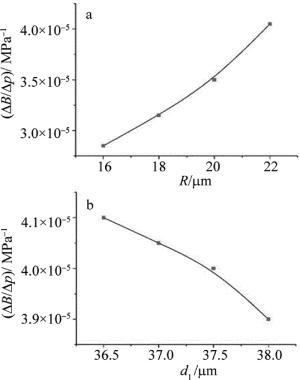
Figure 9. Relationship between phase mode birefringence sensitivity and different parameters R and d1
随着所施加压力的增加,双折射呈线性关系逐渐增加,增加幅度与改变的参量有关,边孔空气孔R和d1对双折射有显著的影响。由图 9可知,当R增加时,相位模式双折射灵敏度逐渐增加,当d1增加时,相位模式双折射灵敏度逐渐减小。
-
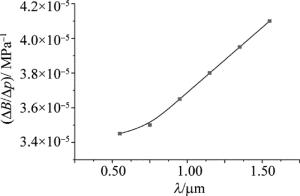
p=200MPa时,不同λ下的相位模式双折射灵敏度随λ的变化如图 10所示。
随着所施加压力的增加,双折射也线性关系逐渐增加,增加幅度与改变的参量有关,自由空间波长λ对双折射有显著的影响。由图 10可知,当λ增加时,相位模式双折射灵敏度逐渐增加。
-
由以上分析可知,边孔空气孔的大小和位置对相位模式双折射灵敏度影响最大。自由空间波长λ越大,相位模式双折射灵敏度越大。近芯区大空气孔d2越小,相位模式双折射灵敏度越大。当椭圆芯区a=1.65μm,b=0.45μm,近芯区d2=0.8μm,d3=1μm,自由空间波长λ=1.55μm,D=125μm,Λ=3.3μm,d/Λ=0.6,R=22μm,d1=36.5μm,X2=0.8μm,Y2=1.3μm,X3=1.9μm,Y3=0.6μm,N=4时,在压力为200MPa条件下,双折射高达1.61×10-2,相位模式双折射灵敏度高达4.1×10-5 MPa-1。由(6)式可知,偏振相位灵敏度高达166.2rad/(MPa·m)。
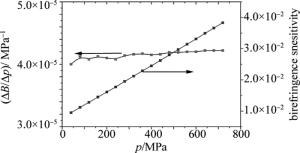
图 11为上述参量下,所施加压力从0MPa增加到720MPa,步长为40MPa,相位模式双折射灵敏度和双折射随着施加压力变化的关系图。本文中的模型所能施加的最大压力为720MPa,且其双折射与所施加压力呈线性关系,相位模式双折射灵敏度基本保持在4.1×10-5 MPa-1左右,该传感器结构在测量范围内性能较为稳定。
-
首先定义了高双折射PCF压力传感计算模型,其次分析了所提出的压力传感结构特性,其中主要分析了几何结构和空间波长对相位模式双折射灵敏度的影响。数值计算表明,本文中提出的PCF结构在没有外界干扰情况下,边孔空气孔的大小和位置、自由空间波长λ和近芯区大空气孔d2对相位模式双折射灵敏度特性都有较大的影响。
在今后的研究中,可在对压力传感特性进行分析时,改变施加压力特性,如非线性施加压力、动态压力及瞬态压力施加方法,最终提出一套可以产业化的传感参量方案。
光子晶体光纤高灵敏度压力传感特性研究
Study on high sensitivity pressure sensing characteristics of photonic crystal fiber
-
摘要: 为了提高压力传感器的灵敏度,利用光子晶体光纤理论及其高双折射特性和可灵活设计的结构特点,设计了一种新型边孔高双折射光子晶体光纤压力传感结构。采用全矢量有限元法并结合COMSOL软件对传感结构的受力和模场分布进行仿真分析,获得压力传感特性随几何结构和自由空间波长的变化关系,通过优化设计得到最优结构参量,进一步获得高压力灵敏度。结果表明,在最优结构下,自由空间波长为1.55μm、压力为200MPa时,偏振相位灵敏度为166.2rad/(MPa·m),所能施加的最大压力为720MPa,相位模式双折射灵敏度保持在4.1×10-5MPa-1左右。该研究对提高压力传感器的灵敏度是有帮助的。Abstract: In order to improve the sensitivity of a pressure sensor, a novel pressure sensing structure of photonic crystal fiber with side hole and high birefringence was designed, based on the theory of photonic crystal fiber and its high birefringence and flexible design structure. The force and mode field distribution of sensing structure were simulated and analyzed by using full vector finite element method and COMSOL software. The dependence of pressure sensing characteristics on geometrical structure and free space wavelength was obtained. The optimum structural parameters were obtained by optimum design. The high pressure sensitivity was further obtained. The results show that, under the optimal structure, when free space wavelength is 1.55μm and pressure is 200MPa, polarization phase sensitivity is 166.2rad/(MPa·m) and maximum pressure that can be applied is 720MPa. The sensitivity of phase mode birefringence is maintained at about 4.1×10-5MPa-1. The research is helpful to improve the sensitivity of pressure sensors.
-
-
[1] YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics [J]. Physical Review Letters, 1987, 58(20): 2059-2062. doi: 10.1103/PhysRevLett.58.2059 [2] JOHN S. Strong localization of photons in certain disordered dielectric superlattices [J]. Physical Review Letters, l997, 58(23): 2486-2489. [3] YU X L, JIANG Y Ch, SONG M Ch. Effect of pressure on the property of the solid-core photonic crystal fibers[J]. Laser Technology, 2008, 32(2):187-190(in Chinese). [4] PARK J, LEE S, KIM S, et al. Enhancement of chemical sensing capability in a photonic crystal fiber with a hollow high index ring defect at the center[J]. Optics & Laser Technology, 2011, 19(3): 1921-1929. [5] YANG Y H, LIU Sh, LU L, et al. Temperature-insensitive pressure sensing technology based on polarization maintaining photonic crystal fiber Sagnac interferometer[J].Infrared and Laser Engineering, 2016, 45(8): 14-19(in Chinese). [6] LÜ J T, WANG Ch M, ZHU Ch H, et al. Dual-core photonic crystal fiber transverse-stress sensor based on surface plasmon resonance[J]. Acta Optica Sinica, 2017, 37(8):828002(in Chinese). doi: 10.3788/AOS [7] LIANG H Q, LIU B, CHEN J, et al. High sensitive elliptic side core surface plasmon resonance refractive index sensing characteristics based on dual-core photonic crystal fiber[J]. Laser & Optoelectronics Progress, 2017, 54(9):90601(in Chinese). [8] ZHANG X D, YUAN M M, CHANG M, et al. Characteristics in square air hole structure photonic crystal fiber[J]. Opto-Electronic Engineering, 2018, 45(5): 170633(in Chinese). [9] PENG R R, LIU B, CHEN J. Study on side-hole surface plasmon resonance refractive index sensing based on single-core photonic crystal optical fiber[J]. Laser Technology, 2018, 42(5): 713-717(in Chinese). [10] LIAO K, LIAO J F, XIE Y M, et al. A defect photonic crystal fiber with high birefringence and negative dispersion[J]. Laser & Optoelectronics Progress, 2018, 55(7): 070604(in Chinese). [11] KRAMER S L B, MELLO M, RAVICHANDRAN G, et al. Phase shifting full-field interferometric methods for determination of in-plane tensorial stress[J]. Experimental Mechanics, 2009, 49(2):303-315. doi: 10.1007/s11340-009-9230-0 [12] LI Zh Zh. Theoretical and experimental research on sensing characteristics of birefringent fiber gratings[D]. Changsha: National University of Defense Technology, 2006: 17-32(in Chinese). [13] QIAN L G. The study on birefringence photonic crystal fiber pressure sensor[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2012: 1-71(in Chinese). [14] LI F Sh, WEI D W, CUI J H, et al. Application and improvement on the optical properties of polycarbonate[J]. Plastics, 2003, 32 (3):65-69(in Chinese). [15] WU G F. The study on birefringence photonic crystal fiber pressure sensor[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2011: 37-48(in Chinese). -
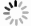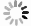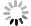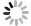

 网站地图
网站地图

 下载:
下载: