-
近年来,激光在遥感、成像、激光通信、微粒捕获、材料热加工等方面[1-5]的应用越来越广泛,众多研究者对激光光束在大气中的传输进行了深入的研究。实际的湍流传输过程中,大气湍流折射率的随机波动,直接影响激光束的传描效率、偏振性、相干性[6]和光束质量[7]。如何提高激光在大气湍流中传输时的光束质量, 一直是专家学者感兴趣的研究课题[8-10]。实验表明,相对于完全相干光而言,部分相干光在湍流传输过程中受湍流影响较小[11]。目前,对于部分相干光在湍流中的理论与实验研究越来越多[12-18],YANG等人研究了部分相干环状偏心光束在海洋湍流中传输的特性[16];SALEM等人研究了部分相干光在大气湍流中的长距离的传输特性[17];WANG等人提出了一种部分相干月牙形矢量光束的模型,从实验上借助于激光二极管(laser diode,LD)光源与透射式空间光调制器(spatial light modulator, SLM)产生了该光束,并用卷积方法对其在Kolmogorov谱中谱密度及光束腰宽演化做了数值分析[18]。
目前的研究表明, 非K谱模型相对于K谱模型,计算结果与实验结果相比参考文献更加吻合[19]。与WANG所使用的方法不同,本文中基于维格纳分布函数的二阶矩定义,利用非K谱模型,对部分相干月牙形光束在大气中传输时的光束腰宽与光束漂移做了相应的计算和分析,最大光强位置的离轴距离的演化规律做了计算和分析。
-
根据维格纳分布函数的二阶矩理论,部分相干月牙形光束在源场的交叉谱密度(cross-spectral density,CSD)函数形式为[18]:
$ \begin{array}{c}{W^{(0)}\left(\boldsymbol{r}_{1}, \boldsymbol{r}_{2}\right)=\tau^{*}\left(\boldsymbol{r}_{1}\right) \tau\left(\boldsymbol{r}_{2}\right) \int p_{1}\left(\boldsymbol{v}_{1}\right) \times} \\ {\exp \left[-\mathrm{i} k\left(\boldsymbol{r}_{2}-\boldsymbol{r}_{1}\right) \cdot \boldsymbol{v}_{1}\right] \mathrm{d}^{2} \boldsymbol{v}_{1}}\end{array} $
(1) 式中,k是波数,r1与r2是传输过程中两个随机的位置矢量,p1(v1)是任意参量v1≡(vx, vy)值的非负函数,τ(r)具有高斯分布[10]:
$ \tau(\boldsymbol{r})=\exp \left(-\frac{\boldsymbol{r}^{2}}{2 \sigma_{0}^{2}}\right) $
(2) 式中,σ0为光腰宽度,p1(v1)为极坐标形式下的可分离函数[18]:
$ p_{1}\left(\boldsymbol{v}_{1}\right)=\frac{k^{2} \delta^{2}\left(k \delta \boldsymbol{v}_{1}\right)^{2 n}}{2^{n} n ! \pi} \exp \left(-\frac{k^{2} \delta^{2} \boldsymbol{v}_{1}^{2}}{2}\right) \cos ^{2}\left(\frac{\boldsymbol{\theta}}{2}\right) $
(3) 式中,λ是波长,n为光束阶数, θ=arctan(vy/vx)表示极坐标中向量v1的方位角, δ为相干长度。
基于广义惠更斯-菲涅耳原理,在z>0的半空间中,光束从源平面处传输到接收平面处的谱密度(spectral density,SD)函数可表示成[10]:
$ \begin{array}{*{20}{c}} {W(\mathit{\boldsymbol{\rho }}, \mathit{\boldsymbol{\rho }}, z) = \frac{1}{{{\lambda ^2}{z^2}}}\smallint \smallint W^{(0)} \left( {{\mathit{\boldsymbol{r}}_1}, {\mathit{\boldsymbol{r}}_2}} \right) \times }\\ {\exp \left( { - \frac{{{\rm{i}}k}}{{2z}}{\mathit{\boldsymbol{r}}_1}^2 + \frac{{{\rm{i}}k}}{z}{\mathit{\boldsymbol{r}}_1} \cdot \mathit{\boldsymbol{\rho }}} \right) \times }\\ {\exp \left( {\frac{{{\rm{i}}k}}{{2z}}{\mathit{\boldsymbol{r}}_2}^2 + \frac{{{\rm{i}}k}}{z}{\mathit{\boldsymbol{r}}_2} \cdot \mathit{\boldsymbol{\rho }}} \right)\left\langle {\exp \left[ {{\mathit{\Psi }^*}\left( {{\mathit{\boldsymbol{r}}_1}, \mathit{\boldsymbol{\rho }}, z} \right) + } \right.} \right.}\\ {{{\left. {\mathit{\Psi }\left( {{\mathit{\boldsymbol{r}}_2}, \mathit{\boldsymbol{\rho }}, z} \right)]} \right\rangle }_m}{{\rm{d}}^2}{\mathit{\boldsymbol{r}}_1}{{\rm{d}}^2}{\mathit{\boldsymbol{r}}_2}} \end{array} $
(4) 式中,ρ是接收平面处某一位置矢量。带有下标m的角括号表示空间-频域中相干理论电场的综合平均,Ψ(r2, ρ, z)是由介质折射率的随机分布引起的复杂相位扰动,Ψ*(r1, ρ, z)表示复共轭,其中各向同性湍流扰动项[10]:
$ \begin{array}{C} {\left\langle {\exp \left[ {{\mathit{\Psi }^*}\left( {{\mathit{\boldsymbol{r}}_1}, \mathit{\boldsymbol{\rho }}, z} \right) + \mathit{\Psi }\left( {{\mathit{\boldsymbol{r}}_2}, \mathit{\boldsymbol{\rho }}, z} \right)} \right]} \right\rangle _m} = \\ \exp \left[ { - \frac{{{{\left( {{\mathit{\boldsymbol{r}}_2} - {\mathit{\boldsymbol{r}}_1}} \right)}^2}}}{{{\rho _0}^2}}} \right] \end{array} $
(5) 式中,ρ02=3/(2π2k2Tz)为空间相干半径,取决于湍流功率谱的选择。
湍流函数T可以表示为:
$ T = \int_0^\infty {{\kappa ^3}} {\mathit{\Phi }_n}(\kappa ){\rm{d}}\kappa $
(6) 湍流谱为:
$ \begin{array}{*{20}{c}} {{\mathit{\Phi }_n}(\kappa ) = A(\alpha ){{\tilde C}_n}^2{\zeta ^2}{{\left( {{\zeta ^2}{\kappa _{xy}}^2 + {\kappa _z}^2 + {\kappa _0}^2} \right)}^{ - \frac{\alpha }{2}}} \times }\\ {\quad \exp \left( { - \frac{{{\zeta ^2}{\kappa _{xy}}^2 + {\kappa _z}^2}}{{{\kappa _m}^2}}} \right), (\kappa > 0, 3 < \alpha < 5)} \end{array} $
(7) 式中,$ \kappa=\sqrt{\zeta^{2}\left({\kappa_x}^{2}+{\kappa_y}^{2}\right)+{\kappa_z}^{2}}=\sqrt{\zeta^{2} {\kappa_x y}^{2}+{\kappa_z}^{2}}$,κ0=2π/L0, κm=C(α)/l0,l0是湍流内尺度,L0是湍流外尺度,$ {\tilde C_n}^2 = \beta {C_n}^2$是结构常数,α为湍流参量,β为量纲常数,ζ为各向异性参量。
$ \begin{array}{c}{C(\alpha)=\left\{\pi A(\alpha) \Gamma\left(\frac{3}{2}-\frac{\alpha}{2}\right)\left(\frac{3-\alpha}{3}\right)\right\}^{\frac{1}{\alpha-5}}}, \\ {(3<\alpha<5)}\end{array} $
(8) $ A(\alpha)=\frac{\Gamma(\alpha-1)}{4 \pi^{2}} \cos \left(\alpha \frac{\pi}{2}\right), (3<\alpha<5) $
(9) 式中,Γ为伽马函数。
把(7)式代入(6)式,得:
$ \begin{array}{*{20}{l}} {T = \int_\infty ^0 {{\kappa ^3}} {\mathit{\Phi }_n}(\kappa ){\rm{d}}\kappa = {\zeta ^{2 - \alpha }}\frac{{A(\alpha )}}{{2(\alpha - 2)}}\frac{{{C_n}^2}}{{{\zeta ^2}}} \times }\\ {\left[ {\frac{{{\kappa _m}^{2 - \alpha }}}{{{\zeta ^2}}}\beta \exp \left( {\frac{{{\kappa _0}^2}}{{{\kappa _m}^2}}} \right)\Gamma \left( {2 - \frac{\alpha }{2}, \frac{{{\kappa _0}^2}}{{{\kappa _m}^2}}} \right) - 2\frac{{{\kappa _m}^{4 - \alpha }}}{{{\zeta ^2}}}} \right]} \end{array} $
(10) $ \beta=2 \frac{{\kappa_0}^{2}}{\zeta^{2}}-2 \frac{{\kappa_m}^{2}}{\zeta^{2}}+\alpha \frac{{\kappa_m}^{2}}{\zeta^{2}} $
(11) (5) 式等号右边可表示为:
$ \begin{array}{c}{\exp \left[-\frac{\left(\boldsymbol{r}_{2}-\boldsymbol{r}_{1}\right)^{2}}{{\rho_0}^{2}}\right]=\int p_{2}\left(\boldsymbol{v}_{2}\right) \times} \\ {\exp \left[-\mathrm{i} k\left(\boldsymbol{r}_{2}-\boldsymbol{r}_{1}\right) \cdot \boldsymbol{v}_{2}\right] \mathrm{d}^{2} \boldsymbol{v}_{2}}\end{array} $
(12) 式中,p2(v2)=k2ρ02exp(-k2ρ02v22/2)/(2π)。
引入下列代换式:
$ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_{\rm{d}}} = {\mathit{\boldsymbol{r}}_2} - {\mathit{\boldsymbol{r}}_1}}\\ {{\mathit{\boldsymbol{r}}_{\rm{s}}} = \left( {{\mathit{\boldsymbol{r}}_2} + {\mathit{\boldsymbol{r}}_1}} \right)/2} \end{array}} \right. $
(13) 将(1)式、(2)式、(3)式、(5)式、(10)式、(12)式以及(13)式带入(4)式中,经过积分运算得:
$ \begin{array}{c}{\langle I(\boldsymbol{\rho}, z)\rangle=\frac{1}{\lambda^{2} z^{2}} \iiint A^{*}\left(\boldsymbol{r}_{\mathrm{s}}-\frac{\boldsymbol{r}_{\mathrm{d}}}{2}\right) A\left(\boldsymbol{r}_{\mathrm{s}}+\frac{\boldsymbol{r}_{\mathrm{d}}}{2}\right) \times} \\ {p_{1}\left(\boldsymbol{v}_{1}\right) p_{2}\left(\boldsymbol{v}_{2}\right) \exp \left(-\frac{\mathrm{i} k}{z} \boldsymbol{r}_{\mathrm{d}} \cdot \boldsymbol{\rho}\right) \times} \\ {\quad \exp \left[-\mathrm{i} k \boldsymbol{r}_{\mathrm{d}} \cdot\left(\boldsymbol{v}_{1}+\boldsymbol{v}_{2}\right)\right] \mathrm{d}^{2} \boldsymbol{r}_{\mathrm{s}} \mathrm{d}^{2} \boldsymbol{r}_{\mathrm{d}} \mathrm{d}^{2} \boldsymbol{v}_{1} \mathrm{d}^{2} \boldsymbol{v}_{2}}\end{array} $
(14) 式中,A被定义为A(r)=τ(r)exp[ikr2/(2z)],将A以及A*分别表示成它们的傅里叶变换形式:
$ \left\{ {\begin{array}{*{20}{l}} {A\left( {{\mathit{\boldsymbol{r}}_{\rm{s}}} + \frac{{{\mathit{\boldsymbol{r}}_{\rm{d}}}}}{2}} \right) = {{\left( {\frac{k}{{2\pi }}} \right)}^2}\int {\tilde A\left( {{\mathit{\boldsymbol{u}}_1}} \right) \times } }\\ {\exp \left[ {{\rm{i}}k{\mathit{\boldsymbol{u}}_1} \cdot \left( {{\mathit{\boldsymbol{r}}_{\rm{s}}} + \frac{{{\mathit{\boldsymbol{r}}_{\rm{d}}}}}{2}} \right)} \right]{{\rm{d}}^2}{\mathit{\boldsymbol{u}}_1}}\\ {{A^*}\left( {{\mathit{\boldsymbol{r}}_{\rm{s}}} - \frac{{{\mathit{\boldsymbol{r}}_{\rm{d}}}}}{2}} \right) = {{\left( {\frac{k}{{2\pi }}} \right)}^2}\int {{{\tilde A}^*}} \left( {{\mathit{\boldsymbol{u}}_2}} \right) \times }\\ {\exp \left[ { - {\rm{i}}k{\mathit{\boldsymbol{u}}_2} \cdot \left( {{\mathit{\boldsymbol{r}}_{\rm{s}}} - \frac{{{\mathit{\boldsymbol{r}}_{\rm{d}}}}}{2}} \right)} \right]{{\rm{d}}^2}{\mathit{\boldsymbol{u}}_2}} \end{array}} \right. $
(15) 有u1=u2=u, 将(15)式带入(14)式,并对rs, rd与u积分可得:
$ \begin{aligned}\langle I(\boldsymbol{\rho}, z)\rangle &=\frac{1}{\lambda^{2} z^{2}} \iiiint\left|\tilde{A}\left(\boldsymbol{v}_{1}+\boldsymbol{v}_{2}+\frac{\boldsymbol{\rho}}{z}\right)\right|^{2} \times \\ & p_{1}\left(\boldsymbol{v}_{1}\right) p_{2}\left(\boldsymbol{v}_{2}\right) \mathrm{d}^{2} \boldsymbol{v}_{1} \mathrm{d}^{2} \boldsymbol{v}_{2} \end{aligned} $
(16) 式中,$\tilde{A}(\boldsymbol{u})=\int A(\boldsymbol{r}) \exp (-\mathrm{i} k \boldsymbol{r} \cdot \boldsymbol{u}) \mathrm{d} \boldsymbol{r} $。
将p1(v1), p2(v2)与$\tilde{A}(\boldsymbol{u}) $带入(16)式,并对v2积分可得:
$ \begin{aligned}\langle I(\boldsymbol{\rho}, z)\rangle &=\frac{1}{F(z)} \frac{k^{2} {\boldsymbol{\rho}_0}^{2}}{2 M_{1}} \frac{k^{2} \delta^{2}(k \delta)^{2 n}}{2^{n} n ! \pi} \exp \left(-\frac{M_{2}}{{\sigma_0}^{2}} \boldsymbol{\rho}^{2}\right) \times \\ & \int {\boldsymbol{v}_1}^{2 n} \exp \left[-\left(\frac{M_{2} z^{2}}{{\sigma_0}^{2}}+\frac{k^{2} \delta^{2}}{2}\right) {\boldsymbol{v}_1}^{2}\right] \times \\ & \exp \left(-\frac{2 M_{2} z}{{\sigma_0}^{2}} \boldsymbol{\rho} \cdot \boldsymbol{v}_{1}\right) \cos ^{2}\left(\frac{\theta}{2}\right) \mathrm{d}^{2} \boldsymbol{v}_{1} \end{aligned} $
(17) 式中,$F(z)=1+\frac{z^{2}}{k^{2} {\sigma_0}^{4}}, M_{1}=\frac{z^{2}}{{\sigma_0}^{2} F(z)}+\frac{k^{2} {\rho_0}^{2}}{2} $$ M_2=\frac{1}{F(z)}\left[1-\frac{z^{2}}{{\sigma_0}^{2} F(z) M_{1}}\right]$。
将(17)式由直角坐标转化到极坐标, 对v1与θ积分,将得到在各向异性湍流中传输的月牙形光束的平均光强的解析表达式:
$ \begin{array}{*{20}{c}} {\langle I(\mathit{\boldsymbol{\rho }}, z)\rangle = \frac{1}{{F(z)}}\frac{{{k^2}{\rho _0}^2}}{{2{M_1}}}\frac{{{k^2}{\delta ^2}{{(k\delta )}^{2n}}}}{{{2^n}n!}} \times }\\ {{\exp \left( { - \frac{{{M_2}}}{{{\sigma _0}^2}}{\mathit{\boldsymbol{\rho }}^2}} \right)\exp ( - t)\left\{ {\frac{1}{2}n!{{\left( {\frac{{2{\sigma _0}^2}}{{2{M_2}{z^2} + {k^2}{\sigma _0}^2{\delta ^2}}}} \right)}^{n + 1}}{{\rm{L}}_1} - } \right.}} \\ {\left. {\frac{1}{2}\left( {n - \frac{1}{2}} \right)!\frac{{{M_2}z}}{{{\sigma _0}^2}}\mathit{\boldsymbol{\rho }}{{\left( {\frac{{2{\sigma _0}^2}}{{2{M_2}{z^2} + {k^2}{\sigma _0}^2{\delta ^2}}}} \right)}^{n + 3/2}}{{\rm{L}}_2}\cos \phi } \right\}} \end{array} $
(18) 式中,Ln0表示广义拉盖尔函数,L1=Ln0(t), L2=Ln-1/21(t), t=-2M22z2ρ2/[σ02(2M2z2+k2σ02δ2)]。
对(17)式做计算,得出光束在传输横截面上方均根束宽为:
$ {W_{{\rm{LT}}}}(z) = \frac{{{\sigma _0}}}{z}\sqrt {\frac{1}{{{M_2}}}} = \sqrt {\frac{1}{{{k^2}{\sigma _0}^2}} + \frac{{{\sigma _0}^2}}{{{z^2}}} + \frac{{4{\pi ^2}Tz}}{3}} $
(19) 从(19)式可知,方程右侧平方根第1项表示光束在自由空间中传输时由σ0所引起的衍射;第2项表示光束在自由空间中传输时只与初始参量和传播距离有关,且其与传输距离的平方成反比;第3项表示各向异性湍流引起的衍射。在湍流函数T=0的自由空间中,w(z)由无穷大降至一常数1/(kσ0)。当光束的传输距离很短时,光束受到各向异性湍流引起的衍射可以忽略不计;随着传输距离的增加,由各向异性湍流引起的衍射项将起着主导作用,因为(19)式中第3项值与z成正比,而第2项的值与z的平方成反比。
-
ANDREWS和PHILIPS基于几何光学近似和Rytov近似,引入高斯滤波函数得到漂移模型为[19]:
$ \begin{aligned}\left\langle {r_\mathrm{c}}^{2}\right\rangle &= 4 \pi k^{2} W_{\mathrm{FS}}^{2}(L) \int_{0}^{L} \int_{0}^{\infty} \kappa \mathit{\Phi}_{n}(\kappa) H_{\mathrm{LS}}(\kappa, z) \times \\ &\left\{1-\exp \left[-\frac{\mathit{\Lambda} L \kappa^{2}(1-z / L)^{2}}{k}\right]\right\} \mathrm{d} \kappa \mathrm{d} z \end{aligned} $
(20) 式中,
$ \left\{ {\begin{array}{*{20}{l}} {{H_{{\rm{LS}}}}(\kappa , z) = \exp \left[ { - {\kappa ^2}{W_{{\rm{LT}}}}^2(z)} \right]}\\ {\mathit{\Lambda } = \frac{{2L}}{{k{W_{{\rm{FS}}}}^2(L)}}}\\ {1 - \exp \left[ { - \frac{{\mathit{\Lambda }L{\kappa ^2}{{(1 - z/L)}^2}}}{k}} \right] \simeq \frac{{\mathit{\Lambda }L{\kappa ^2}{{(1 - z/L)}^2}}}{k}} \end{array}} \right. $
(21) 式中,L为发射端和接收端之间的距离,WFS(L)表示自由空间下的光束宽度,HLS(κ, z)是大标量滤波函数,WLT(z)表示湍流下的光束宽度,Λ表示无量纲参量,则:
$ \begin{array}{*{20}{c}} {\left\langle {{r_{\rm{c}}}^2} \right\rangle = 4\pi k{W_{{\rm{FS}}}}^2(L)A(\alpha )\overline {{{\tilde C}_n}^2} \mathit{\Lambda }L{\zeta ^{2 - \alpha }} \times }\\ {\int_0^\infty {{\kappa ^3}} {{\left( {{{\tilde \kappa }_0}^2 + {\kappa ^2}} \right)}^{ - \frac{\alpha }{2}}}\exp \left[ { - {\kappa ^2}\left( {\frac{1}{{{{\tilde \kappa }_m}^2}} + } \right.} \right.}\\ {\left. {\left. {{W_{{\rm{LT}}}}^2(z)} \right)} \right]{\rm{d}}\kappa \int_0^L {{{\left( {1 - \frac{z}{L}} \right)}^2}} {\rm{d}}z} \end{array} $
(22) 将(7)式代入(22)式,经过计算得:
$ \begin{array}{*{20}{c}} {\left\langle {{r_{\rm{c}}}^2} \right\rangle = \frac{{8\pi {L^2}A(\alpha )\overline {{{\tilde C}_n}^2} {\zeta ^{2 - \alpha }}}}{{2( - 2 + \alpha )}} \times }\\ {\Gamma \left[ {2 - \frac{\alpha }{2}, {\kappa _0}^2\left( {\frac{{\rm{d}}}{{{\zeta ^2}}} + \frac{1}{{{\kappa _m}^2}}} \right)} \right]\int_0^L {{{(1 - z/L)}^2}} {\rm{d}}z \times }\\ {\left\{ { - 2{{\tilde \kappa }_0}^{4 - \alpha } + {{\tilde \kappa }_m}^2\exp \left[ {{\kappa _0}^2\left( {\frac{d}{{{\zeta ^2}}} + \frac{1}{{{\kappa _m}^2}}} \right)} \right]{{\left( {d + \frac{1}{{{{\tilde \kappa }_m}^2}}} \right)}^{\alpha /2 - 2}} \times } \right.}\\ {\left. {\left( {\frac{{2d{\kappa _0}^2}}{{{\kappa _m}^2}} + \frac{{2{\kappa _0}^2}}{{{{\tilde \kappa }_m}^2{\kappa _m}^2}} + \frac{{ - 2 + \alpha }}{{{{\tilde \kappa }_m}^2}}} \right)} \right\}} \end{array} $
(23) 式中, d=WLT2(z), κm=C(α)/l0, κ0=2π/L0,$ {\tilde{C}_n}^{2}=\beta {C_n}^{2}, \beta=2 {\tilde{\kappa}_0}^{2}-2 {\tilde{\kappa}_m}^{2}+\alpha {\tilde{\kappa}_m}^{2}, {\tilde{\kappa}_0}=\kappa_{0} / \zeta, {\tilde{\kappa}_m}=\kappa_{m} / \zeta, r_{\mathrm{c}}$即表示部分相干月牙形光束在非K谱中的光束漂移。
-
(18) 式、(19)式以及(23)式是本文中经计算得到的几个重要公式,从(18)式可得到部分相干月牙形光束传输时光强分布的演化规律。以下参量皆选为:λ=532nm,n=3,δ=2mm, σ0=50mm,l0=1m,L0=0.01m,ζ=0.8,α=3.5,Cn2=5×10-13m-2/3。
图 1a~图 1d中给出了在自由空间中月牙形光束传输至不同距离处的归一化光强分布。随着传输距离的增大,光强从源平面中的高斯分布逐渐演化为月牙形分布。图 1e~图 1f中给出了在Cn2=5×10-13m-2/3的各向异性湍流中,月牙形光束传输至不同距离处的归一化光强分布,当距离小于0.5km时,光强分布与自由空间相似,然而对于较大的距离,由于大气湍流的影响,光强从月牙形分布逐渐变回高斯分布。图 1中色柱表示3维坐标系中正值与颜色图的映射关系。

Figure 1. Normalized intensity distribution of partially coherent crescent-like beam at different distances
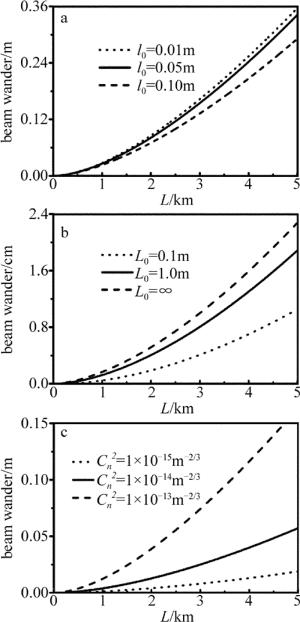
图 2a表示各向异性参量ζ不同时,部分相干月牙形光束在各向异性湍流中传输时漂移的变化曲线。由图所示,ζ较小的部分相干月牙形光束的漂移的值大于ζ较大的漂移的值,说明各向异性参量较大时,光束漂移受湍流影响较小。当ζ=1时,各向异性湍流变为各向同性湍流,由图可知,各向异性湍流较各向同性湍流对漂移的影响较小。图 2b中给出了湍流参量α对月牙形光束的漂移的影响。随着α的增大,部分相干月牙形光束的漂移先增加到最大值再逐渐下降,α的值为11/3时漂移达到最大值。
图 3a中给出不同的湍流内尺度对部分相干月牙形光束的漂移的影响。湍流内尺度较小的部分相干月牙形光束的漂移的值大于湍流内尺度较大的漂移的值,表明湍流内尺度较大时,光束漂移受湍流影响较小。图 3b中给出不同的湍流外尺度对光束漂移的影响。湍流外尺度较大时,光束漂移受湍流影响较大。图 3c表示湍流结构常数不同时,部分相干月牙形光束的漂移在各向异性湍流中传输变化曲线。随着传输距离的增加,月牙形光束的漂移逐渐増大,湍流结构常数越大,光束漂移越大。
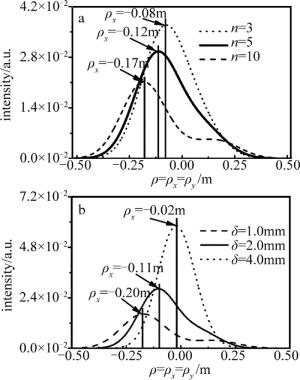
图 4a是当λ=532nm,δ=2mm,σ0=50mm时,非K谱中光束阶数n对部分相干月牙形光束的光强分布的影响。可以看出,最大光强位置离轴距离随着n的增大而增大。当n取3,5和10时,最大光强位置分别位于-0.08m,-0.12m,-0.17m处,离轴距离分别为0.08m,0.12m,0.17m。图 4b是不同相干长度δ对光强分布的影响,当n=3,λ=532nm,σ0=50mm时,最大光强位置离轴距离随着δ的增大而减小。当δ取1.0mm,2.0mm和4.0mm时,离轴距离分别为0.20m,0.11m,0.02m。
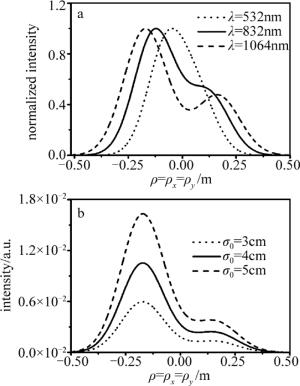
图 5a是当n=3,δ=2mm,σ0=50mm时,非K谱中波长λ对部分相干月牙形光束的归一化光强的影响。由图可知,最大光强位置的离轴距离随着波长的增大而增大,光束越发散。图 5b是当n=3,δ=1mm,σ0=50mm时,非K谱中光腰宽度σ0对光强分布的影响。随着σ0的增加,部分相干月牙形光束的光强增大,而最大光强位置不变,最大光强位置的离轴距离保持不变。
-
基于广义惠更斯-菲涅耳原理,推导了部分相干月牙形光束在非K谱中平均光强、光束腰宽和光束漂移的解析表达式,并进行相应的数值计算,得到了部分相干月牙形光束在非K谱模型的漂移规律,光束漂移随着各向异性参量的增大,湍流内尺度的增大,湍流外尺度的减小,结构常数的减小而降低;与各向同性湍流相比,各向异性湍流对光束漂移的影响较小;月牙形光束的最大光强位置的离轴距离分别随着波长、光束阶数的增大而增大,随着相干长度的增大而减小等规律,计算所得结果对实际光束传输有一定的理论参考价值。
部分相干月牙形光束在非Kolmogorov谱中的漂移
Beam wander of a partially coherent crescent-like beam in non-Kolmogorov turbulence
-
摘要: 为了探究部分相干月牙形光束在非Kolmogorov谱中漂移的演化规律, 采用拓展Huygens-Fresnel原理, 得到了相应的解析表达式, 并运用MATLAB进行了数值模拟。结果表明, 在非Kolmogorov谱中, 部分相干月牙形光束的漂移分别随着各向异性参量的增大、湍流内尺度的增大、湍流外尺度的减小、结构常数的减小而降低; 与各向同性湍流相比, 各向异性湍流对漂移的影响较小; 月牙形光束的最大光强位置的离轴距离分别随着波长、光束阶数的增大而增大, 随着相干长度的增大而减小。月牙形光束由于最大光强位置的离轴特性, 有利于绕过障碍物传输, 所得结论对实际光通信有一定参考价值。Abstract: In order to investigate the evolution of beam wander of partially coherent crescent beams in non-Kolmogorov turbulence, the extended Huygens-Fresnel principle was used and the corresponding analytical expressions were obtained. Numerical simulation was carried out by using MATLAB. The results show that, in the non-Kolmogorov turbulence, beam wander of partially coherent crescent-like beams decreases with the increase of anisotropic parameters, the increase of turbulent inner scale, the decrease of turbulent outer scale and the decrease of structural constants respectively. Compared with isotropic turbulence, anisotropic turbulence has little effect on beam wander. Off-axis distance of the maximum intensity position of crescent-like beam increases with the increase of wavelength and beam order respectively. It decreases with the increase of coherence length. Off-axis characteristic at the position of the maximum intensity is beneficial for crescent-like beams to transmit around obstacles. The obtained conclusions have some reference value for practical optical communication.
-
-
[1] CHEN Y H, WANG F, LIU L, et al. Generation and propagation of a partially coherent vector beam with special correlation functions. Physical Review, 2014, A89(1): 1-11. [2] CAI Y J, HE S L. Partially coherent flattened Gaussian beam and its paraxial propagation properties. Journal of the Optical Society of America, 2006, A23(10): 2623-2628. [3] NELSON M, AVRAMOV Z S, KOROTKOVA O, et al. Scintillation reduction in pseudo multi-Gaussian Schell-model beams in the maritime environment. Optics Communications, 2016, 364:145-149. doi: 10.1016/j.optcom.2015.11.049 [4] FEI J C, CUI Z F, WANG J S, et al. Propagation characteristics of elegant Laguerre-Gaussian beam passing through a circular aperture in turbulent atmosphere. Laser Technology, 2011, 35(6): 849-853 (in Chinese). [5] LIANG C, WANG F, LIU X, et al. Experimental generation of cosine-Gaussian-correlated Schell-model beams with rectangular symmetry. Optics Letters, 2014, 39(4):769-772. doi: 10.1364/OL.39.000769 [6] GBUR G. Partially coherent beam propagation in atmospheric turbulence. Journal of the Optical Society of America, 2014, A31(9):2038-2045. [7] WEN W, JIN Y, HU M J, et al. Beam wander of coherent and partially coherent Airy beam arrays in a turbulent atmosphere. Optics Communications, 2018, 415:48-55. doi: 10.1016/j.optcom.2018.01.033 [8] VOELZ D, XIAO X, KOROTKOVA O. Numerical modeling of Schell-model beams with arbitrary far-field patterns. Optics Letters, 2015, 40(3):352-355. doi: 10.1364/OL.40.000352 [9] GORI F, SANTARSUERO M. Devising genuine spatial correlation functions. Optics Letters, 2007, 32(24):3531-3533. doi: 10.1364/OL.32.003531 [10] WANG F, KOROTKOVA O. Convolution approach for beam propagation in random media. Optics Letters, 2016, 41(7):1546-1549. doi: 10.1364/OL.41.001546 [11] ZHONG Y L, CUI Z F, SHI J P, et al. Propagation properties of partially coherent flat-topped beam array in a turbulent atmosphere. Laser Technology, 2010, 34(4):542-547(in Chinese). [12] XU K T, YUAN Y SH, FENG X, et al. Propagation properties of partially coherent flat-topped beam array in oceanic turbulence. Laser Technology, 2015, 39(6):877-884(in Chinese). [13] ZHAO Q, HAO H Y, FAN H Y, et al. Focusing characteristics of partially coherent cosh-Gaussian beams propagation through turbulent atmosphere. Laser Technology, 2016, 40(5): 750-755(in Chinese). [14] CAI Y. Generation of various partially coherent beams and their propagation properties in turbulent atmosphere: A review. Progress in Electromagnetics Research Symposium Proceedings, 2011, 7924(2): 170-180. [15] GBUR G, WOLF E. Spreading of partially coherent beams in random media. Journal of the Optical Society of America, 2002, A19(8):1592-1598. [16] YANG T, JI X L, LI X Q. Propagation characteristics of partially coherent decentred annular beams propagating through oceanic turbulence. Acta Physica Sinica, 2015, 64(20):204206(in Chinese). [17] SALEM M, SHIRAI T, DOGARIU A, et al. Long-distance propagation of partially coherent beams through atmospheric turbulence. Optics Communications, 2003, 216:261-265. doi: 10.1016/S0030-4018(02)02340-4 [18] WANG F, LI J, PIEDRA M, et al. Propagation dynamics of partially coherent crescent-like optical beams in free space and turbulent atmosphere. Optics Express, 2017, 25(21): 26055-26066. doi: 10.1364/OE.25.026055 [19] FENG J X, YUAN Y Sh, QU J, et al. Beam wander of multi-Gaussian schell-model hermite-Gaussian beam in atmospheric turbulence. Progress in Electromagnetics Research Symposium Proceedings, 2017, 22(19): 311-316. -

 网站地图
网站地图

 下载:
下载: