网站地图
下载:
-
激光束在光学成像、激光遥感、光互联和自由空间光通信等方面有大量的应用，使得激光束在大气湍流中的研究受到国内外学者的广泛关注[1-6]。但是由于大气湍流的存在，激光束在大气中传输时不可避免地受到湍流的影响，发生光束漂移[7-9]、光束质量[10]、强度[11-12]、相干性[13]和偏振性[14]变化等一系列的湍流效应，使得激光束的光束质量大大降低，因此寻找合适的激光束以减小大气湍流对光束的影响是众多学者一直努力的方向。参考文献[13]中研究了部分相干高斯-谢尔光束在大气湍流中的传输特性，发现一定条件下部分相干光与完全相干光相比，它受大气湍流的影响更小。参考文献[14]中提出矢量涡旋光束在大气中传输时，受到湍流的干扰相对小。自1987年DURNIN首次提出了近似无衍射光束的概念并在实验中产生了这种新型的光束[15]以来，这种新型的光束便引起了众多学者的兴趣。1996年研究人员发现当贝塞尔光束的中心光斑被遮挡后，经过很小的一段距离就可以恢复的自愈合特性[16-19]。参考文献[20]中从理论上推导了贝塞尔光束在大气湍流中的光束漂移模型，计算了不同湍流强度下高阶贝塞尔光束的光束漂移，结果表明, 在相同的大气湍流条件下，高阶贝塞尔光束受大气湍流的影响较小, 因此, 研究贝塞尔光束在大气湍流中的传输性质对于自由空间光通信等诸多方面有很重要的意义。鉴于此，本文中基于拓展的惠更斯-菲涅耳原理和维格纳分布函数的二阶矩定义理论上推导了受遮挡贝塞尔-高斯光束在大气湍流中的质量因子解析式，进行相应的数值计算，分析了湍流大气结构常数、湍流内标量、遮挡物尺寸和束腰宽度对受遮挡贝塞尔-高斯光束的质量因子的影响。
-
在柱坐标下，参考文献[3]中给出了贝塞尔-高斯光束在源平面的(z=0)的电场强度分布表达式，在光束的中心加一个障碍物即高斯吸收函数[17]，则其在源平面的电场强度分布函数可以表示为:
$ \begin{array}{*{20}{c}} {{E_0}\left( {\rho , \varphi , 0} \right) = {{\rm{J}}_{\rm{m}}}\left( {\frac{R}{{{w_0}^2}}\rho } \right)\exp \left( { - \frac{{{\rho ^2}}}{{{w_0}^2}}} \right) \times }\\ {\exp \left( { - {\rm{i}}m\varphi } \right)\left[ {1 - \exp \left( { - \frac{{{\rho ^2}}}{{R_0^2}}} \right)} \right]} \end{array} $
(1) 源平面上交叉谱密度函数可以表示为:
$ \begin{array}{*{20}{c}} {W\left( {{\rho _1},{\rho _2},0} \right) = {{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _1}} \right){{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _2}} \right) \times }\\ {\exp \left[ { - \frac{{\rho _1^2 + \rho _2^2}}{{{w_0}^2}} - {\rm{i}}m\left( {{\varphi _1} - {\varphi _2}} \right)} \right] + {{\rm{J}}_m}\left( {\frac{R}{{{w_0}^2}}{\rho _1}} \right) \times }\\ {{{\rm{J}}_m}\left( {\frac{R}{{{w_0}^2}}{\rho _2}} \right)\exp \left[ { - \frac{{\rho _1^2 + \rho _2^2}}{{{w_1}^2}} - {\rm{i}}m\left( {{\varphi _1} - {\varphi _2}} \right)} \right] - }\\ {{{\rm{J}}_m}\left( {\frac{R}{{{w_0}^2}}{\rho _1}} \right){{\rm{J}}_m}\left( {\frac{R}{{{w_0}^2}}{\rho _2}} \right) \times }\\ {\exp \left[ { - \frac{{\rho _1^2}}{{w_0^2}} - \frac{{\rho _2^2}}{{w_1^2}} - {\rm{i}}m\left( {{\varphi _1} - {\varphi _2}} \right)} \right] - }\\ {{{\rm{J}}_m}\left( {\frac{R}{{{w_0}^2}}{\rho _1}} \right){{\rm{J}}_m}\left( {\frac{R}{{{w_0}^2}}{\rho _2}} \right) \times }\\ {\exp \left[ { - \frac{{\rho _1^2}}{{w_1^2}} - \frac{{\rho _2^2}}{{w_0^2}} - {\rm{i}}m\left( {{\varphi _1} - {\varphi _2}} \right)} \right]} \end{array} $
(2) 式中，Jm表示m阶第1类贝塞函数，w0为基模高斯光束的束腰宽度，参量R=kw02sinφ，φ表示在傍轴上理想贝塞尔场的锥角，$k = \frac{{2{\rm{ \mathit{ π} }}}}{\lambda } $表示波数，λ为光束的波长，R0为遮挡物半径，ρi=(ρxi, ρyi)=(ρicosφi, ρisinφi)表示源平面中任意的两个点，φ表示沿z方向的角，$w_1^2 = \frac{{R_0^2 + w_0^2}}{{w_0^2R_0^2}} $。在(2)式中取:
$ \begin{array}{*{20}{c}} {{W_1}\left( {{\rho _1},{\rho _2},0} \right) = {{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _1}} \right){{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _2}} \right) \times }\\ {\exp \left[ { - \frac{{\rho _1^2 + \rho _2^2}}{{{w_0}^2}} - {\rm{i}}m\left( {{\varphi _1} - {\varphi _2}} \right)} \right],}\\ {{W_2}\left( {{\rho _1},{\rho _2},0} \right) = {{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _1}} \right){{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _2}} \right) \times }\\ {\exp \left[ { - \frac{{\rho _1^2 + \rho _2^2}}{{{w_1}^2}} - {\rm{i}}m\left( {{\varphi _1} - {\varphi _2}} \right)} \right],}\\ {{W_3}\left( {{\rho _1},{\rho _2},0} \right) = {{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _1}} \right){{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _2}} \right) \times }\\ {\exp \left[ { - \frac{{\rho _1^2}}{{w_0^2}} - \frac{{\rho _2^2}}{{w_1^2}} - {\rm{i}}m\left( {{\varphi _1} - {\varphi _2}} \right)} \right],}\\ {{W_4}\left( {{\rho _1},{\rho _2},0} \right) = {{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _1}} \right){{\rm{J}}_\mathit{m}}\left( {\frac{R}{{{w_0}^2}}{\rho _2}} \right) \times }\\ {\exp \left[ { - \frac{{\rho _1^2}}{{w_1^2}} - \frac{{\rho _2^2}}{{w_0^2}} - {\rm{i}}m\left( {{\varphi _1} - {\varphi _2}} \right)} \right]} \end{array} $
(3) 根据参考文献[5]，可得W1(ρ1, ρ2, 0)的表达式。为简单起见，引入新的积分变量ρ=(ρ1+ρ2)/2, ρd=ρ1－ρ2，可得: ${W_{1\theta \theta \mathit{'}}}\left( {{\rho _1},{\rho _2},0} \right) \Rightarrow {W_{1\theta \theta \mathit{'}}}\left( {\rho ,{\rho _{\rm{d}}},0} \right) $。
$ \begin{array}{*{20}{c}} {{W_{1\theta \theta '}}\left( {\rho , {\rho _{\rm{d}}}, 0} \right) = }\\ {\exp \left[ { - \frac{{2{\rho ^2}}}{{w_0^2}} - \frac{{\rho _{\rm{d}}^2}}{{2w_0^2}} + {\rm{i}}\left( {{\mathit{\boldsymbol{Q}}_ - } \cdot \rho + \frac{{{\mathit{\boldsymbol{Q}}_ + } \cdot {\rho _{\rm{d}}}}}{2}} \right)} \right]} \end{array} $
(4) 式中，2维矢量${\mathit{\boldsymbol{Q}}_ \pm } = \frac{R}{{w_0^2}}\left( {\cos \theta \pm \cos \theta \mathit{', }{\rm{sin}}\theta \pm {\rm{sin}}\theta \mathit{'}} \right) $，θ和θ′是积分公式与贝塞尔函数之间转换引入的无关变量。
激光从源平面(z=0)出发，在湍流大气中传输时，参考文献[14]中给出了光束在z平面的表达式，在此引入新的积分变量$\mathit{\boldsymbol{r = }}\frac{{{\mathit{\boldsymbol{r}}_1} + {\mathit{\boldsymbol{r}}_2}}}{2}, {\mathit{\boldsymbol{r}}_{\rm{d}}} = {\mathit{\boldsymbol{r}}_1} - {\mathit{\boldsymbol{r}}_2} $, 其中，r1和r2表示接收面上任意的两个点，垂直于光束的传播方向, 得:
$ \begin{array}{*{20}{c}} {\left\langle {{W_{1\theta \theta '}}\left( {\mathit{\boldsymbol{r}}, {\mathit{\boldsymbol{r}}_{\rm{d}}}, z} \right)} \right\rangle = }\\ {{{\left( {\frac{1}{{2{\rm{ \mathit{ π} }}}}} \right)}^2}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{{\rm{d}}^2}\rho '{{\rm{d}}^2}{\mathit{\boldsymbol{\kappa }}_{\rm{d}}}} } } } \times }\\ {\left\langle {{W_{1\theta \theta '}}\left( {\rho ', {\mathit{\boldsymbol{r}}_{\rm{d}}} + \frac{z}{k}{\mathit{\boldsymbol{\kappa }}_{\rm{d}}}, 0} \right)} \right\rangle \times }\\ {\exp \left[ { - {\rm{i}}\mathit{\boldsymbol{r}} \cdot {\mathit{\boldsymbol{\kappa }}_{\rm{d}}} + {\rm{i}}\rho ' \cdot {\mathit{\boldsymbol{\kappa }}_{\rm{d}}} - } \right.}\\ {\left. {H\left( {{\mathit{\boldsymbol{r}}_{\rm{d}}}, {\mathit{\boldsymbol{r}}_{\rm{d}}} + \frac{z}{k}{\mathit{\boldsymbol{\kappa }}_{\rm{d}}}, z} \right)} \right]} \end{array} $
(5) 式中, κd是空间频域的位置矢量, H表示湍流影响。对无关变量ρ′进行积分并整合得到:
$ \begin{array}{*{20}{c}} {\left\langle {{W_{1\theta \theta '}}\left( {\mathit{\boldsymbol{r}}, {\mathit{\boldsymbol{r}}_{\rm{d}}}, z} \right)} \right\rangle = \frac{{w_0^2}}{{8{\rm{ \mathit{ π} }}}}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\exp \left( { - {\rm{i}}\mathit{\boldsymbol{r}} \cdot {\mathit{\boldsymbol{\kappa }}_{\rm{d}}}} \right) \times } } }\\ {\exp \left[ { - \frac{{w_0^2\mathit{\boldsymbol{Q}}_ - ^2}}{8} - \frac{1}{{2w_0^2}}\mathit{\boldsymbol{r}}_{\rm{d}}^2 + \frac{{{\rm{i}}{\mathit{\boldsymbol{Q}}_ + }}}{2} \cdot {\mathit{\boldsymbol{r}}_{\rm{d}}} - } \right.}\\ {\left. {H\left( {{\mathit{\boldsymbol{r}}_{\rm{d}}}, {\mathit{\boldsymbol{r}}_{\rm{d}}} + \frac{z}{k}{\mathit{\boldsymbol{\kappa }}_{\rm{d}}}, z} \right)} \right] \times }\\ {\exp \left[ { - \left( {\frac{{w_0^2}}{8} + \frac{{{z^2}}}{{2w_0^2{k^2}}}} \right)\mathit{\boldsymbol{\kappa }}_{\rm{d}}^2 + } \right.}\\ {\left. {\left( {\frac{{{\rm{i}}{\mathit{\boldsymbol{Q}}_ + }z}}{{2k}} - \frac{{w_0^2{\mathit{\boldsymbol{Q}}_ - }}}{4} - \frac{z}{{kw_0^2}} \cdot {\mathit{\boldsymbol{r}}_{\rm{d}}}} \right) \cdot {\mathit{\boldsymbol{\kappa }}_{\rm{d}}}} \right]{{\rm{d}}^2}{\mathit{\boldsymbol{\kappa }}_{\rm{d}}}} \end{array} $
(6) 受遮挡贝塞尔-高斯光束在大气湍流中传输时，其维格纳分布函数可以表示为:
$ \begin{array}{*{20}{c}} {h\left( {\mathit{\boldsymbol{r}}, \varphi , z} \right) = }\\ {\int_0^{2{\rm{ \mathit{ π} }}} {\int_0^{2{\rm{ \mathit{ π} }}} {{\rm{d}}\theta {\rm{d}}\theta '\exp \left[ { - {\rm{i}}m\left( {\theta - \theta '} \right)} \right]{h_{\theta \theta '}}\left( {\mathit{\boldsymbol{r}}, \varphi , z} \right)} } } \end{array} $
(7) 其中,
$ \begin{array}{*{20}{c}} {{h_{\theta \theta '}}\left( {\mathit{\boldsymbol{r}}, \varphi , z} \right) = {{\left( {\frac{k}{{2{\rm{ \mathit{ π} }}}}} \right)}^2}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{W_{\theta \theta '}}\left( {\mathit{\boldsymbol{r}}, {\mathit{\boldsymbol{r}}_{\rm{d}}}, z} \right)} } \times }\\ {\exp \left( { - {\rm{i}}k{\mathit{\boldsymbol{r}}_{\rm{d}}} \cdot \varphi } \right){{\rm{d}}^2}{\mathit{\boldsymbol{r}}_{\rm{d}}} = }\\ {D\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{{\rm{d}}^2}{\mathit{\boldsymbol{r}}_{\rm{d}}}{{\rm{d}}^2}{\mathit{\boldsymbol{\kappa }}_{\rm{d}}}{\mathit{\Lambda }_{\theta \theta '}}\left( {{\mathit{\boldsymbol{r}}_{\rm{d}}}, {\mathit{\boldsymbol{r}}_{\rm{d}}}, z} \right)} } } } \times }\\ {\exp \left( { - {\rm{i}}k{\mathit{\boldsymbol{r}}_{\rm{d}}} \cdot \varphi - {\rm{i}}{\mathit{\boldsymbol{\kappa }}_{\rm{d}}} \cdot \mathit{\boldsymbol{r}}} \right)} \end{array} $
(8) 式中, $D = \frac{{{k^2}w_0^2}}{{8{{\rm{ \mathit{ π} }}^3}}} $，φ=(φx, φy)表示这个矢量沿z方向的角，kφx, kφy分别表示沿x轴和y轴方向的波矢量分量, Λθθ′是引入的一个函数，是W1θθ′对ρ′进行积分后取得的一个函数。
由于维格纳分布函数的性质及(n1+n1+m1+m2)阶矩定义[10]，可得:
$ \begin{array}{*{20}{c}} {{{\left\langle {{x^2} + {y^2}} \right\rangle }_1} = {f_1}\left[ {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_m}\left( {{\gamma _1}} \right){g_1} + } \right.}\\ {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_{m + 1}}\left( {{\gamma _1}} \right)\left( {\frac{{{R^2}{z^2}}}{{4\omega _0^4{k^2}}}} \right) + \exp \left( { - {\gamma _1}} \right) \times }\\ {{{\rm{I}}_{m - 1}}\left( {{\gamma _1}} \right)\left( {\frac{{{R^2}{z^2}}}{{4\omega _0^4{k^2}}}} \right) + \exp \left( { - {\gamma _1}} \right){{\rm{I}}_{m + 1}}\left( {{\gamma _1}} \right)\left( {\frac{{{R^2}}}{{16}}} \right) + }\\ {\left. {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_{m - 1}}\left( {{\gamma _1}} \right)\left( {\frac{{{R^2}}}{{16}}} \right)} \right], }\\ {{{\left\langle {x{\varphi _x} + y{\varphi _y}} \right\rangle }_1} = {f_1}\left[ {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_m}\left( {{\gamma _1}} \right){j_1} + } \right.}\\ {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_{m + 1}}\left( {{\gamma _1}} \right)\left( {\frac{{{R^2}z}}{{4\omega _0^4{k^2}}}} \right) + }\\ {\left. {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_{m - 1}}\left( {{\gamma _1}} \right)\left( {\frac{{{R^2}z}}{{4\omega _0^4{k^2}}}} \right)} \right], }\\ {{{\left\langle {\varphi _x^2 + \varphi _y^2} \right\rangle }_1} = {f_1}\frac{{w_0^2}}{{8{\rm{ \mathit{ π} }}}}\left[ {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_m}\left( {{\gamma _1}} \right){v_1} + } \right.}\\ {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_{m + 1}}\left( {{\gamma _1}} \right)\left( {\frac{{{R^2}}}{{4\omega _0^4{k^2}}}} \right) + }\\ {\left. {\exp \left( { - {\gamma _1}} \right){{\rm{I}}_{m - 1}}\left( {{\gamma _1}} \right)\left( {\frac{{{R^2}}}{{4\omega _0^4{k^2}}}} \right)} \right]} \end{array} $
(9) 式中，Im表示m阶修正的贝塞尔函数和。
$ \left\{ \begin{array}{l} {f_1} = \frac{{{{\left( {2{\rm{ \mathit{ π} }}} \right)}^6}w_0^2D}}{{8{\rm{ \mathit{ π} }}{k^2}}}\\ {\gamma _1} = \frac{{{R^2}}}{{4w_0^2}}\\ {g_1} = \left( {\frac{{w_0^2}}{2} + \frac{{2{z^2}}}{{w_0^2{k^2}}} + \frac{{4{{\rm{ \mathit{ π} }}^2}{z^3}T}}{3} + } \right.\\ \;\;\;\;\;\;\left. {\frac{{{R^2}{z^2}}}{{2w_0^4{k^2}}} - \frac{{{R^2}}}{8}} \right)\\ {j_1} = \left( {\frac{{2z}}{{w_0^2{k^2}}} + 2{{\rm{ \mathit{ π} }}^2}{z^2}T + \frac{{{R^2}z}}{{2w_0^4{k^2}}}} \right)\\ {v_1} = \left( {\frac{{2z}}{{w_0^2{k^2}}} + 4{{\rm{ \mathit{ π} }}^2}zT + \frac{{{R^2}}}{{2w_0^4{k^2}}}} \right) \end{array} \right. $
(10) 式中，T是与空间功率谱函数相关的一个参量。同理可以求出W2(ρ1, ρ2, 0), W3(ρ1, ρ2, 0), W4(ρ1, ρ2, 0)的参量组合。根据魏格纳分布函数的二阶矩理论，可以分析光束束宽〈x2+y2〉1/2和光束发散角〈φx2+φy2〉1/2的变化规律，同时可以求出非零交叉项〈xφx+yφy〉1/2，由光束束宽，光束发散角和非零交叉项，受遮挡贝塞尔-高斯光束的M2因子为[10, 21]:
$ \begin{array}{*{20}{c}} {{M^2}\left( z \right) = }\\ {k{{\left( {\left\langle {{r^2}} \right\rangle + \left\langle {{\varphi ^2}} \right\rangle - {{\left\langle {r\varphi } \right\rangle }^2}} \right)}^{1/2}} = }\\ {k\left\{ {\left[ {{{\left\langle {{x^2} + {y^2}} \right\rangle }_1} + {{\left\langle {{x^2} + {y^2}} \right\rangle }_2} + {{\left\langle {{x^2} + {y^2}} \right\rangle }_3} + } \right.} \right.}\\ {\left. {{{\left\langle {{x^2} + {y^2}} \right\rangle }_4}} \right] \times \left[ {{{\left\langle {\varphi _x^2 + \varphi _y^2} \right\rangle }_1} + {{\left\langle {\varphi _x^2 + \varphi _y^2} \right\rangle }_2} + } \right.}\\ {\left. {{{\left\langle {\varphi _x^2 + \varphi _y^2} \right\rangle }_3} + {{\left\langle {\varphi _x^2 + \varphi _y^2} \right\rangle }_4}} \right] - \left[ {{{\left\langle {x{\varphi _x} + y{\varphi _y}} \right\rangle }_1} + } \right.}\\ {{{\left\langle {x{\varphi _x} + y{\varphi _y}} \right\rangle }_2} + {{\left\langle {x{\varphi _x} + y{\varphi _y}} \right\rangle }_3} + }\\ {{{\left. {{{\left. {{{\left\langle {x{\varphi _x} + y{\varphi _y}} \right\rangle }_4}} \right]}^2}} \right\}}^{1/2}}} \end{array} $
(11) -
(11) 式是本文中的主要解析表达式，它可以方便地研究受遮挡贝塞尔-高斯光束在大气湍流中的质量因子，利用MATHEMATIC软件，相应数值计算结果见下。
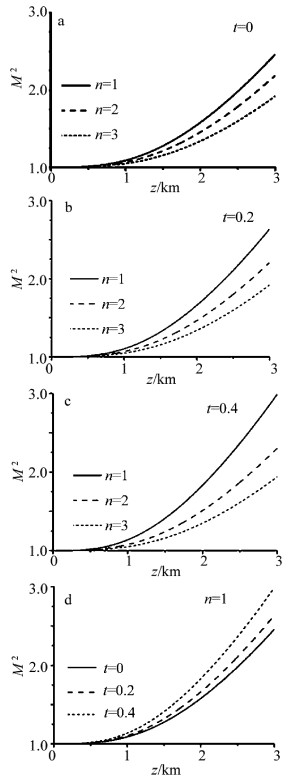
图 1中给出了遮挡参量t不同时, 不同拓扑荷数n所对应的归一化M2因子的特性曲线(w0=5mm, λ=632.8nm, l0=5mm, R=6w0)。遮挡物的半径R0=tw0，t表示遮挡物大小与贝塞尔-高斯光束光斑大小的关系。图 1反映出当遮挡参量不变时，贝塞尔-高斯光束归一化的M2因子随着拓扑荷数的增大而减小；当拓扑荷数不变时，随着遮挡参量的增大，贝塞尔-高斯光束归一化的M2因子也在增大。
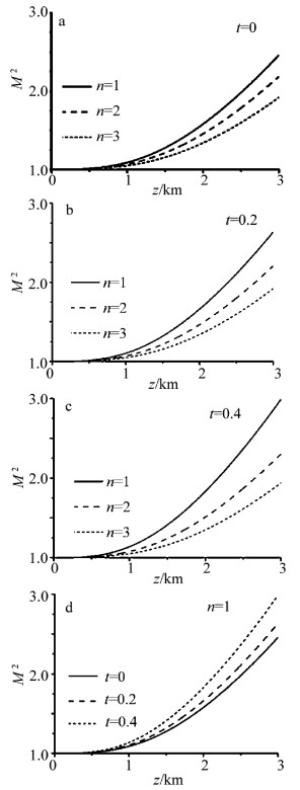
Figure 1. The normalized M2 factor of Bessel-Gaussian beam with different topological charges and obstacle parameters
图 2中给出了遮挡参量不同时, 不同光束腰宽对归一化M2因子的影响特性(n=1, l0=5mm, λ=632.8nm, R=6w0, R0=tw0, Cn2=10－16m－2/3)。计算结果表明，当遮挡参量不变时，贝塞尔-高斯光束归一化的M2因子随着腰宽的增大而减小；当腰宽不变时，随着遮挡参量的增大，贝塞尔-高斯光束归一化的M2因子也在增大。
Figure 2. The normalized M2 factor of Bessel-Gaussian beam with different waist widths and obstacle parameters
图 3中计算了选择不同的遮挡参量和不同湍流内标量时，归一化M2因子的变化规律(n=1, w0=5mm, λ=632.8nm, R=6w0, R0=tw0, Cn2=10－16m－2/3)。图 3反映出当遮挡参量不变时，贝塞尔-高斯光束归一化的M2因子随着湍流内标量的增大而减小；当湍流内标量不变时，随着遮挡参量的增大，贝塞尔-高斯光束归一化的M2因子也在增大的规律。
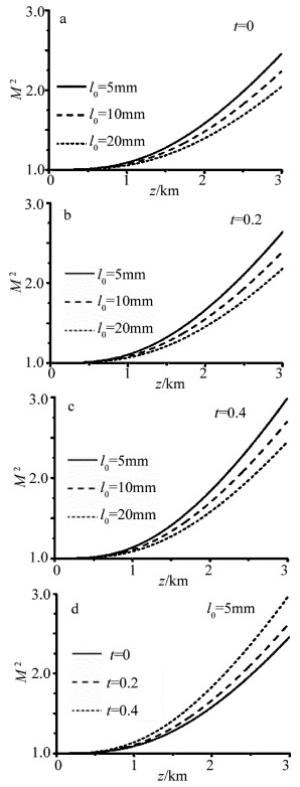
Figure 3. The normalized M2 factor of Bessel-Gaussian beam with different inner scales and obstacle parameters
当改变遮挡参量和湍流大气结构常数时，归一化M2因子的变化曲线见图 4(n=1, l0=5mm, w0=5mm, R=6w0, R0=tw0, λ=632.8nm)。图 4很明显反映出当遮挡参量不变时，贝塞尔-高斯光束归一化的M2因子随着湍流大气结构常数的增大而增大；当湍流大气结构常数不变时，贝塞尔-高斯光束归一化的M2因子随着遮挡参量的增大而增大的现象。
Figure 4. The normalized M2factor of Bessel-Gaussian beam with different structure constants and obstacle parameters
-
基于拓展的惠更斯-菲涅耳原理和维格纳分布函数的二阶矩定义，理论推导了受遮挡贝塞尔-高斯光束在湍流大气传输中M2因子的解析表达式，分析了遮挡参量、传播距离、湍流内标量、束腰宽度和湍流结构常数等参量对受限贝塞尔-高斯光束质量因子的影响。数值计算和分析表明, 当遮挡物的尺寸为零，即不加障碍物时，其传输质量因子随传播距离、湍流大气结构常数的增大而增大，随着腰宽、湍流内标量、光束拓扑荷数的增大而减小，而当遮挡物尺寸不大于0.4倍的腰宽时，该光束的传输质量因子也呈现相同的变化规律，但随着遮挡物尺寸的增大，贝塞尔-高斯光束需要自愈合的距离更远，在大气湍流扰动下，其传输质量因子也更大。
受遮挡贝塞尔-高斯光束在湍流大气传输的M2因子
M2 factor of disturbed Bessel-Gaussian beam propagating in turbulent atmosphere
-
摘要: 为了研究受遮挡贝塞尔-高斯光束在湍流大气中传输时质量因子的特性，基于拓展的惠更斯-菲涅耳原理和维格纳分布函数的二阶矩定义，经理论推导得出受遮挡贝塞尔-高斯光束的解析表达式，并进行了相应的数值计算。结果表明，当遮挡物尺寸不大于0.4倍的腰宽时，受遮挡贝塞尔-高斯光束在湍流大气中的传输质量因子随传播距离、湍流大气结构常数的增大而增大，随着湍流内标量、光束拓扑荷数的增大而减小。在相同条件下，光束的传输质量因子随着遮挡物尺寸的增大而增大。所得结论对实际激光传输和自由空间光通信有一定的参考价值。
-
关键词:
- 大气与海洋光学 /
- M2因子 /
- 拓展的惠更斯-菲涅耳原理 /
- 贝塞尔-高斯光束
Abstract: In order to study the propagation properties of the disturbed Bessel-Gaussian beam in turbulent atmosphere, based on the extended Huygens-Fresnel principle and the second-order moments of the Wigner distribution function, the formulas of M2 factor for the disturbed Bessel-Gaussian beam were derived by theoretical calculation analysis, and the corresponding numerical calculation was carried out. The results show that, when the size of obstruction is not more than 0.4 times of beam width, the propagation factor of Bessel-Gaussian beam in turbulent atmosphere would increase with the increasing of the propagation distance and atmospheric structure constant, and decrease with the increasing of the inner scale of turbulence and topological charge indexes. Under the same condition, the propagation factor of Bessel-Gaussian beam in turbulent atmosphere increases with the increase of the size of obstruction. These results have certain reference value in free space optical communication and actual laser transmission. -
Figure 1. The normalized M2 factor of Bessel-Gaussian beam with different topological charges and obstacle parameters
Figure 2. The normalized M2 factor of Bessel-Gaussian beam with different waist widths and obstacle parameters
Figure 3. The normalized M2 factor of Bessel-Gaussian beam with different inner scales and obstacle parameters
-
[1] NIU H H, HAN Y P. Performance analysis of Bessel-Gaussian vortex beam propagation in atmospheric turbulence[J]. Laser Technology, 2017, 41(3):451-455(in Chinese). [2] ZHU Y, CHEN M Y, ZHANG Y X, et al. Propagation of the OAM mode carried by partially coherent modified Bessel-Gaussian beams in an anisotropic non-Kolmogorov marine atmosphere[J]. Journal of the Optical Society of America, 2016, A33(12):2277-2283. [3] ZHU K C, LI S X, TANG Y, et al. Study on the propagation parameters of Bessel-Gaussian beams carrying Optical vortices through atmospheric turbulence[J]. Journal of the Optical Society of America, 2012, A29(3):251-257. [4] NELSON W, PALASTRO J P, DAVIS C C. Propagation of Bessel and Airy beams through atmospheric turbulence[J]. Journal of the Optical Society of America, 2014, A 31(3):603-609. [5] WANG X Y, YAO M W, QIU Z L, et al. Evolution properties of Bessel-Gaussian Schell-model beams in non-Kolmogorov turbulence[J]. Optics Express, 2015, 23(10):12508-12523. doi: 10.1364/OE.23.012508 [6] XU K T, YUAN Y H, FENG X, et al. Propagation properties of partially coherent flat-topped beam array in oceanic turbulence[J]. Laser Technology, 2015, 39(6):877-884(in Chinese). [7] WU Y Q, ZHANG Y X, LI Y. Beam wander of Gaussian-Schell model beams propagating through oceanic turbulence[J]. Optics Communications, 2016, 371:59-66. doi: 10.1016/j.optcom.2016.03.041 [8] DAN Y Q, ZHANG B. Second moments of partially coherent beams in atmospheric turbulence[J].Optics Letters, 2009, 34(5):563-565. doi: 10.1364/OL.34.000563 [9] ZHAO Q, ZHONG M, LÜ B D. Experimental study about laser beam wander in atmosphere[J]. Laser Technology, 2010, 34(4):532-534(in Chinese). [10] DAN Y Q, ZHANG B. Beam propagation factor of partially coherent flat-topped beams in a turbulent atmosphere[J]. Optics Express, 2008, 16(20):15563-15575. doi: 10.1364/OE.16.015563 [11] BIRCH P, ITUEN I. Long-distance Bessel beam propagation through Kolmogorov turbulence[J]. Journal of the Optical Society of America, 2015, A32(11):2066-2073. [12] YANG G C, HAN S C, LIU X C, et al. Scintillation and dancing of laser beam propagation in marine atmosphere[J]. Laser Technology, 1991, 15(2):104-107(in Chinese). [13] WU J. Propagation of a Gaussian-Schell beam through turbulent media[J]. Journal of Modern Optics, 1990, 37(4):671-684. doi: 10.1080/09500349014550751 [14] CHENG W, HAUS J W, ZHAN Q W. Propagation of vector vortex beams through a turbulent atmosphere[J]. Optics Express, 2009, 17(20):17829-17836. doi: 10.1364/OE.17.017829 [15] DURNIN J, MICELI J, EBERLY J. Diffraction-free beams[J]. Physical Review Letters, 1987, 58(15):1499-1501. doi: 10.1103/PhysRevLett.58.1499 [16] QIAO C H, FENG X X, CHU X X. Propagation and self-healing ability of a Bessel-Gaussian beam modulated by Bessel gratings[J]. Optics Communications, 2016, 365:24-28. doi: 10.1016/j.optcom.2015.11.079 [17] CHU X X, WEN W. Quantitative description of the self-healing ability of a beam[J]. Optics Express, 2014, 22(6):6899-6904. doi: 10.1364/OE.22.006899 [18] CHENG M J, GUO L X, LI J T. Propagation properties of an optical vortex carried by a Bessel-Gaussian beam in anisotropic turbulence[J]. Journal of the Optical Society of America, 2016, A33(8):1442-1450. [19] LI S H, WANG J. Adaptive free-space optical communications through turbulence using self-healing Bessel beams[J]. Scientific Reports, 2017(7):43233. [20] YUAN Y S, LEI T, LI Z H, et al. Beam wander relieved orbital angular momentum communication in turbulent atmosphere using Bessel beams[J]. Scientific Reports, 2017(7):42276. [21] SERNA J, MARTÍNEZ-HERRERO R, MEJÍAS P M. Parametric characterization of general partially coherent beams propagating through ABCD optical systems[J]. Journal of the Optical Society of America, 1991, A8(8):1094-1098. -
点击查看大图
图(4)
计量
- 文章访问数: 7314
- HTML全文浏览量: 5869
- PDF下载量: 217
- 被引次数: 0
