网站地图
下载:
-
矢量光场是一种近年来受到广泛关注的新型激光场，其偏振态在横向传输截面上呈局域化非均匀分布。矢量光场的空间光强与偏振具备空域的可调控性，可充分利用各种灵活的调控方式进行调控，丰富了激光的输出特征，在激光技术领域有着重要应用前景。矢量光场经紧聚焦后的聚焦场具有独特的矢量化特征，其聚焦特性在多个领域获得了深入的研究[1-4]，如光学微纳捕获与操控[5-7]、光学微加工[8-9]、光学信息存储[10-11]以及光学显微成像技术[12]等领域。
作为近轴波动方程(paraxial wave equation，PWE)在椭圆坐标系下准确正交解的第3类完整解系，Ince-Gaussian(IG)模式是Hermite-Gaussian(HG)和Laguerre-Gaussian(LG)模式之间的连续过渡模式[13]。IG激光模式在2004年由BANDRES等人提出并在实验上获得验证[14-16]。IG模式由于可以转换成LG模式和HG模式，是一种更具有普遍性的激光模式，有望在微粒操控[17-18]、生物医学[19]、光学通信[20-21]、量子信息处理等方面获得有更广阔的应用。近年来，基于IG模式的标量光场已经进行了较为系统的研究[13]。IG模式的产生主要有两类方式:一类是被动(腔外)产生方式，包括使用液晶器件和数字微镜器件(digital micromirror device, DMD)等方式；另一类是主动(腔内)产生方式，主要是通过打破谐振腔的对称性和控制光的增益和损耗来直接产生。具有复杂空间模结构复杂涡旋和奇点IG模式的生成为量子信息处理提供了有效操控对象。IG模式也在生物细胞激光器领域被发现，证实其是自然存在的一种基本辐射模式[19]。但需要指出的是，作为结构光场重要特性之一的偏振特性，在IG模式模式光场中的研究尚未充分，正开始受到关注。IG模式激光不仅包含奇模和偶模，而且不同椭圆参数的IG模式光强分布也不相同，由IG模式获得的新型矢量光场在紧聚焦条件下会表现出丰富的光学结构。如最近报道的Ince-Gaussian矢量激光场，在复杂偏振态中发现了嵌入式的扩展奇点网络结构，其偏振矢量结构被证实具有空间稳定性[22]，可推动基于偏振调制的米氏粒子光学捕获[23]。因此，本文中通过Richards-Wolf矢量衍射理论，对IG矢量光场在不同入射条件下的紧聚焦特性进行研究，分析了入射光场束腰位置对聚焦特性的影响，证明了紧聚焦条件下透镜位于一定范围内时横向结构依然保持稳定性，同时纵向偏振分量会对聚焦场的光强结构产生重要影响。
-
在横截面z定义椭圆坐标：x=f(z)coshξcosη，y=f(z)sinhξsinη，其中f(z)是与z有关的半焦距，ξ∈[0, ∞), η∈[0, 2π)分别是径向、角向变量，并且ξ的等值线为共焦的椭圆，η的等值线为共焦的双曲线。近轴波动方程在椭圆坐标系下可以得到两组独立波动方程解，分别为[14, 16]:
$ $\begin{array}{*{20}{c}} {G_{p, m}^{\rm{e}}(r, \varepsilon ) = \frac{{C{w_0}}}{{w(z)}}C_p^m({\rm{i}}\xi , \varepsilon )C_p^m(\eta , \varepsilon )\exp \left[ {\frac{{ - {r^2}}}{{{w^2}(z)}}} \right] \times }\\ {\exp \left\{ {{\rm{i}}\left[ {kz + \frac{{k{r^2}}}{{2R(z)}} - (p + 1){\Psi _{{\rm{GS}}}}(z)} \right]} \right\}} \end{array}$ $
(1) $ $\begin{array}{l} G_{p, m}^{\rm{o}}(r, \varepsilon ) = \frac{{S{w_0}}}{{w(z)}}S_p^m({\rm{i}}\xi , \varepsilon )S_p^m(\eta , \varepsilon )\exp \left[ {\frac{{ - {r^2}}}{{{w^2}(z)}}} \right] \times \\ \;\;\;\;\;\;\exp \left\{ {{\rm{i}}\left[ {kz + \frac{{k{r^2}}}{{2R(z)}} - (p + 1){\mathit{\Psi} _{{\rm{GS}}}}(z)} \right]} \right\} \end{array}$ $
(2) 式中，上标e和o分别表示偶模和奇模，r为半径，C和S为归一化常数，w0为束腰半径，w(z)=w0×$\sqrt {\left({1 + {z^2}/z_{\rm{R}}^2} \right)} $是激光在z处的横截宽度; Cpm(η, ε)和Spm(η, ε)分别表示带有阶数p和级数m的偶次和奇次因斯多项式，p和m满足(－1)p－m=1，即始终具有相同的奇偶性，其中对于偶模0≤m≤p，对于奇模1≤m≤p; ε=2f02/w02是由束腰半径w0和束腰面半焦距f0决定的椭圆参量，其表示椭圆率的变化程度; k是波数; R(z)=z+zR2/z为光波前的曲率半径，－(p+1)×ΨGS(z)=－(p+1)arctan(z/zR)为阶数为p的IG模的Gouy相移，其中ZR=kw02/2为瑞利长度。由于C00(η, ε)=1，因此p=0, m=0时IG模式其实就是最简单的高斯模式[13]。
一般地，柱对称矢量光场可以看成是两个正交偏振分量的叠加[24]。同样，两个具有偶模和奇模IG模式的正交偏振分量的叠加，可以构建具有IG模式的矢量光场，即IGV(Ince-Gaussian vectorial)光场。广义的IGV光场可以用琼斯矢量表示为:
$ {\mathit{\boldsymbol{E}}_{{\rm{IGV}}}}(x, y) = \left[ {\begin{array}{*{20}{c}} {G_{{p_x}, {m_x}, {\varepsilon _x}}^{\rm{e}}}\\ {G_{{p_y}, {m_y}, {\varepsilon _y}}^0\exp ({\rm{i}}\delta )} \end{array}} \right] $
(3) 式中，Gpex, mx, εx, Gopy, my, εy分别是IGV光场的x, y偏振分量，下标px, mx, εx和py, my, εy分别表示IGV光场x分量和y分量IG模式的阶数、级数、椭圆参量，δ是x, y分量之间的初始相位延迟。利用具有不同参量p, m, ε的正交偏振分量，可以构建具有不同强度与偏振分布的复杂矢量结构的IGV光场。为了方便，用EIGV(epxmxεx, opymyεy)来表示由两个正交偏振分量生成的IGV矢量光场。
-
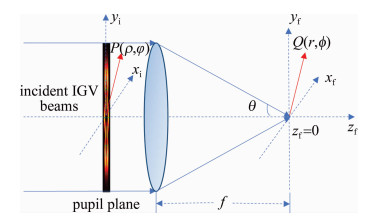
IGV光束的紧聚焦特性可以通过Richards-Wolf矢量衍射方法来进行数值分析[25-26]。图 1为IGV光束的紧聚焦示意图。一个高数值孔径(numerical aperture，NA)的透镜聚焦入射的IGV光束，该透镜满足正弦条件, 半径r=f sinθ(f为焦距)。透镜光瞳面Pi(xi, yi)处的IGV光束经过聚焦之后，在焦点(xf, yf, zf)附近的光场为:
Figure 1. A schematic diagram of tightly focusing IGV beams
$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{E}}\left( {{x_{\rm{f}}}, {y_{\rm{f}}}, {z_{\rm{f}}}} \right) = A\iint_{ - 1}^1 {\frac{1}{{\sqrt {\cos \theta } }} \times } \\ \;\;\;\;\;\;\left\{ {G_{{p_x}, {m_x}, {\varepsilon _x}}^{\rm{e}}\left[ {\begin{array}{*{20}{c}} {\left. {\left( {\cos \theta {{\cos }^2}\varphi + {{\sin }^2}\varphi } \right){\mathit{\boldsymbol{e}}_x}} \right\}}\\ {(\cos \theta \sin \varphi \cos \varphi - \sin \varphi \cos \varphi ){\mathit{\boldsymbol{e}}_y}}\\ {\sin \theta \cos \varphi {\mathit{\boldsymbol{e}}_z}} \end{array}} \right] + } \right.\\ \left. {G_{{p_y}, {m_y}, {\varepsilon _y}}^{\rm{o}}{\rm{exp}}({\rm{i}}\delta )\left[ {\begin{array}{*{20}{c}} {(\cos \theta \sin \varphi \cos \varphi - \sin \varphi \cos \varphi ){\mathit{\boldsymbol{e}}_x}}\\ {\left( {\cos \theta {{\sin }^2}\varphi + {{\cos }^2}\varphi } \right){\mathit{\boldsymbol{e}}_y}}\\ {\sin \theta \sin \varphi {\mathit{\boldsymbol{e}}_z}} \end{array}} \right]} \right\} \times \end{array} \\ \exp \left\{ { - {\rm{i}}k\left[ {r\sin \theta \cos (\varphi - \phi ) + {z_{\rm{f}}}\cos \theta } \right]} \right\}{\rm{d}}{x_{\rm{i}}}{\rm{d}}{y_{\rm{i}}} $
(4) 式中，入射光瞳面处的圆柱坐标系(xi, yi)是由半径$\rho = \sqrt {x_{\rm{i}}^2 + y_{\rm{i}}^2} $和方位角$\varphi = {\tan ^{ - 1}}\left({\frac{{{y_{\rm{i}}}}}{{{x_{\rm{i}}}}}} \right)$表示的，A是积分常数，收敛角θ=sin－1(dNAρ)，其中dNA表示数值孔径，ex，ey和ez分别为x，y和z方向上的单位矢量。聚焦场E(xf, yf, zf)位于由半径$r = \sqrt {x_{\rm{f}}^2 + y_{\rm{f}}^2} $和方位角$\phi = {\tan ^{ - 1}}\left({\frac{{{y_{\rm{f}}}}}{{{x_{\rm{f}}}}}} \right)$表示的笛卡尔坐标系中。这就是一般IGV光束通过高NA透镜聚焦后的聚焦场表达式。
-
设入射IGV矢量光场的束腰位置距离透镜为zi。当入射IGV光场束腰位于聚焦透镜中心处即zi=0时，IGV矢量光场在聚焦过程中将保持结构的稳定性，这在WANG和ZHAN等人的前期工作中已被证实。但对于IGV光场的束腰位置与聚焦场特性之间的关系，尚未进行相关的研究。根据(1)式和(2)式，本文中研究在px=py及δ=0条件下，通过(4)式Richards-Wolf矢量衍射积分理论，对IGV矢量光场在非束腰位置(zi≠0)情况下的紧聚焦特性进行分析。需要说明的是，x, y分量初始相位差δ≠0时，入射IGV光场会失去局域线偏振特性，出现椭圆或圆偏振的局域化分布特征，聚焦后焦平面上也会失去局域化线偏振特征，但在聚焦过程中的光场结构稳定性与束腰位置变之间的规律与δ=0时是一致的，因此本文中仅通过δ=0的情况来予以分析说明。
为不失一般性，本文中入射IG矢量光场取EIGV(e441, o423)为例，即入射光场正交分量的阶数px=py=4, x偏振分量级数mx=4, y偏振分量级数my=2, 椭圆率分别为εx=1和εy=3，聚焦透镜的数值孔径dNA=0.95。这里将zi=0时入射光场分布区域进行了归一化处理，光场分布在边长为1正方形区域。(1)式和(2)式中，入射光束的束腰半径w0取0.4，波长λ=632.8nm，入射IGV光场束腰的位置zi为0, 0.3zR, 0.5zR, 0.7zR，zR。入射IGV光场束腰位置改变时，入射场的光强与偏振态分布，除了放大因子外，在此聚焦过程中基本保持不变，即IG矢量光场在近轴传播情况下存在稳定性。为了避免重复，这里只给出了zi=0时入射光场的光强和偏振分布，如图 2所示。这里需要注意的是，zi=0, 0.3zR, 0.5zR, 0.7zR时入射场的显示区域为[-1, 1]，而入射位置z=zR时入射场显示区域为[-1.5, 1.5]。由于IG模式光束其实也属于高斯类光束，所以在入射位置zi=zR时入射IGV场的光斑大小刚好是zi=0时入射场光斑的2倍，入射光场强度约是zi=0时的一半。
Figure 2. The incident IGV field EIGV (e441, o423) and the corresponding tightly focusing field when the beam waist position zi=0 (dNA=0.95, δ=0)
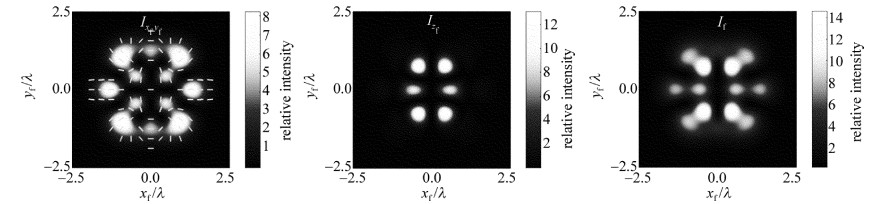
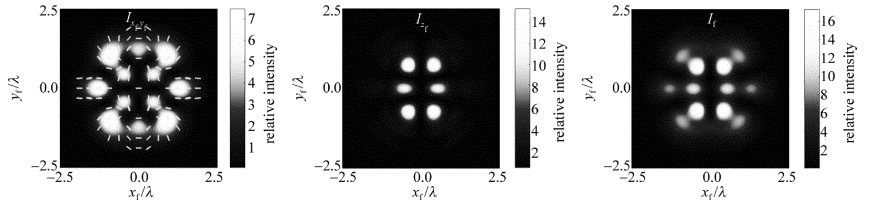
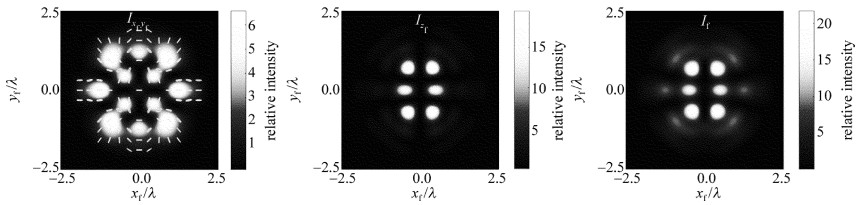
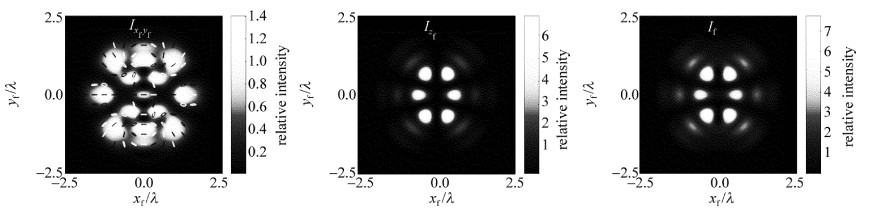
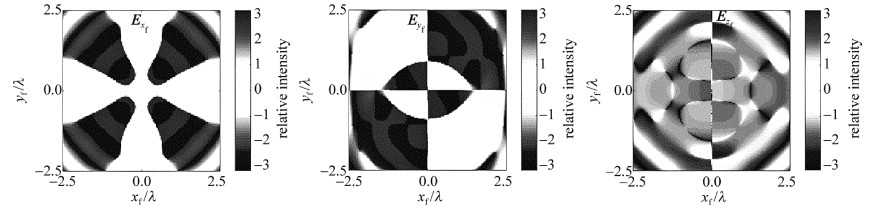
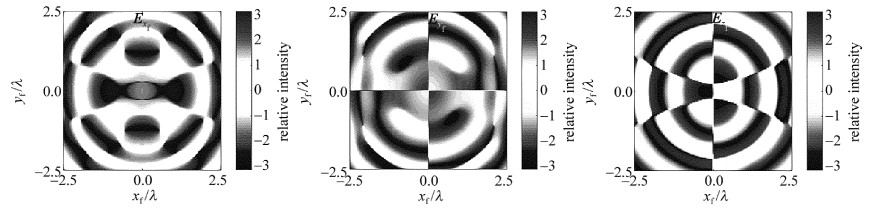
图 2a~图 2c中给出了束腰位置zi=0时入射IGV光场、x偏振分量Exi和y偏振分量Eyi光强结构(Ixiyi, Ixi和Iyi)，及IGV光场的偏振分布。图 2d~图 2f以及图 3~图 6中给出的是在焦平面具有局域偏振方向的横向光强分布(Ixfyf, Izf和If)。比较图 2~图 6中不同束腰位置时对应的焦场光强分布Ixfyf，可以发现：当入射光场束腰位置zi < 0.5zR时，紧聚焦过程中矢量光场的横向光场始终保持了稳定性，横向场的光强分布(Ixfyf)和偏振结构基本与入射光场一致，横向光场分布区域变化不大，但轴向光场(Izf)的聚焦质量会逐渐变差，逐渐出现光晕, 如图 4所示。当入射光场束腰位置zi>0.5zR时，其聚焦场的横向结构矢量特性出现变化，开始出现明显的局域性椭圆偏振，但大体上还是呈现线偏振分布。在入射束腰位置变化到zi=zR时，与入射场相比，聚焦场中的横向场(Ixfyf)的偏振结构和光强分布都发生了明显的畸变。
Figure 3. The corresponding tightly focusing field of the incident IGV light field EIGV (e441, o423) when the beam waist position zi=0.3zR (dNA=0.95, δ=0)
Figure 4. The corresponding tightly focusing field of the incident IGV light field EIGV (e441, o423) when the beam waist position zi=0.5zR (dNA=0.95, δ=0)
Figure 5. The corresponding tightly focusing field of the incident IGV light field EIGV (e441, o423) when the beam waist position zi=0.7zR (dNA=0.95, δ=0)
Figure 6. The corresponding tightly focusing field of the incident IGV light field EIGV (e441, o423) when the beam waist position zi=zR (dNA=0.95, δ=0)
以zi=zR为例，通过聚焦前后光场的相位分布特征的变化，来分析聚焦场横向结构产生局域椭圆偏振的原因。图 7和图 8中分别给出了入射光场束腰位置zi为0和zR时，聚焦场中横向光场和轴向偏振分量的相位分布图。zi=0时，聚焦横向光场的偏振分布为线偏振的原因，是由于聚焦场x, y分量在叠加位置的相位差为0或±π，这一点可以从图 7中聚焦场x偏振分量、y偏振分量Exf和Eyf的相位分布图得出。而zi=zR时，由图 8中Exf，Eyf可以看到, 在焦场x, y两分量叠加位置处会出现相位差为π/4等这类情况，所以在这些位置会出现椭圆偏振。图 6中，浅灰色椭圆表示左旋方向，深灰色椭圆表示右旋方向。其中，可以看到, 聚焦场横截面的局域椭圆偏振态的旋向关于对称轴是相反的。这是因为焦场x分量的相位分布关于坐标轴对称，而y分量相位分布关于坐标轴相反，所以导致垂直叠加后的椭圆偏振旋向相反。
Figure 7. The phase distribution of the polarization components of the focusing field corresponding to EIGV (e441, o423) at the incident waist position zi=0
Figure 8. The phase distribution of the polarization components of the focusing field corresponding to EIGV (e441, o423) at the incident waist position zi=zR
在紧聚焦的条件下，纵向场Izf非常重要，会影响整个聚焦场的分布。从图 2~图 6中的聚焦场光强分布可以发现，纵向场(Izf)随着入射位置zi的增大，其光强图案的变化也越大，特别是在zi>0.5zR时它的光强结构变化得愈发明显。由图 8可以看出，在zi=zR时，纵向场的相位分布不再是每个相邻的区域是相反且呈现±π/2的阶跃式分布(zi=0时)，而是在[-π, π]之间每个区域呈现类环带分布。纵向场结构会对焦点附近的总场图案产生影响。由图 2~图 6中的焦平面总的强度分布If可以看到，由于纵向场光强图案随着zi增大而发生的变化越来越突出，焦场总的光强图案If的变化也越来越明显，特别是在zi>0.5zR时这种现象尤其明显。在zi=zR时，聚焦纵向场分量几乎控制了整个总焦场的光强图案，如图 6所示，整个焦场的总光强图案发生了明显的畸变。
以上以阶数p=4为例进行了IGV光场束腰位置对紧聚焦特性影响的研究。对于其它各阶数和级数的IGV光场，不同参量只会影响光场的复杂程度，但束腰位置改变对聚焦特性的影响规律都是一样的。
-
综上所述，本文中根据矢量光场的衍射积分理论，研究了一种新型的IG矢量光场的聚焦特性，对入射矢量场的束腰位置变化时，IGV光束经过高数值孔径透镜的紧聚焦特性进行了研究。研究结果显示，在紧聚焦条件下，当px=py时，束腰位置在一定范围内的入射光场(zi < 0.5zR)，其IGV横向聚焦场的矢量模式依然保持稳定性。但若束腰位置超过了一定范围(zi>0.5zR)，聚焦横向光场的结构不再保持稳定性。同时，轴向聚焦光场聚焦特性也会随之变化。这项研究工作的结果，将有助于深入理解复杂结构光场的聚焦特性，推进新型矢量光场在微纳尺度的应用基础研究，在多粒子捕获与操控、多自由度信息存储等研究领域提供有用的研究参考价值。
Ince-Gaussian矢量光场束腰位置对紧聚焦特性影响的研究
Research on the effect of waist position changing of Ince-Gaussian vectorial beam on tightly focusing characteristics
-
摘要: 为了获得Ince-Gasussian矢量光场束腰位置对紧聚焦特性的影响规律，采用正交偏振的奇偶模式叠加理论和Richards-Wolf矢量衍射积分理论，对不同束腰位置的Ince-Gaussian矢量光场紧聚焦特性进行了研究。结果表明，在高数值孔径聚焦条件下，入射Ince-Gaussian矢量场的束腰距离透镜位置zi在一定瑞利长度zR范围内(zi < 0.5zR)改变时，其聚焦场的横向场结构即光强与偏振态分布，依然可以保持稳定；通过聚焦场相位结构分析，给出了在束腰距离透镜位置zi超过一定瑞利长度zR范围(zi>0.5zR)时，影响横向场结构不稳定的原因；聚焦场纵向偏振分量作为聚焦场的一个自由度，被证明可以用来构建更加丰富的矢量结构光场。此研究结果对复杂结构矢量光场在光学微操控与光信息存储方面的研究有重要参考价值。
-
关键词:
- 物理光学 /
- 偏振 /
- 矢量光场 /
- 紧聚焦 /
- Ince-Gaussian模式
Abstract: In order to research the influence of the beam waist position on the tightly focusing of the Ince-Gaussian vectorial beam, the superposition theory of orthogonally polarized even and odd modes and the Richards-Wolf vector diffraction integral theory were utilized in this study and the tightly focusing feature of the Ince-Gaussian vectorial beam at the different waist position was analyzed. The results show that under the condition of high numerical aperture focusing, the transverse field structure of the focusing field possessing distribution of light intensity and polarization state can still remain stable when the distance zi between the beam waist position of the Ince-Gaussian vectorial field and the lens changes within a certain Rayleigh length zR (zi < 0.5zR). By analyzing the phase structure of the focusing field, the reason of the instability of the transverse field structure is given when the distance zi between the beam waist position and the lens exceeds a certain Rayleigh length zR (zi>0.5zR). At the same time, the longitudinal polarization component of the focusing field, as a degree of freedom of the focusing field, can be used to construct a more abundant vector structured light field. The results can provide great value for the research of complex structure vector optical field in optical micromanipulation and optical information storage.-
Key words:
- physical optics /
- polarization /
- tightly focusing /
- vector optical field /
- Ince-Gaussian mode
-
Figure 2. The incident IGV field EIGV (e441, o423) and the corresponding tightly focusing field when the beam waist position zi=0 (dNA=0.95, δ=0)
Figure 3. The corresponding tightly focusing field of the incident IGV light field EIGV (e441, o423) when the beam waist position zi=0.3zR (dNA=0.95, δ=0)
Figure 4. The corresponding tightly focusing field of the incident IGV light field EIGV (e441, o423) when the beam waist position zi=0.5zR (dNA=0.95, δ=0)
Figure 5. The corresponding tightly focusing field of the incident IGV light field EIGV (e441, o423) when the beam waist position zi=0.7zR (dNA=0.95, δ=0)
Figure 6. The corresponding tightly focusing field of the incident IGV light field EIGV (e441, o423) when the beam waist position zi=zR (dNA=0.95, δ=0)
Figure 7. The phase distribution of the polarization components of the focusing field corresponding to EIGV (e441, o423) at the incident waist position zi=0
-
[1] CHEN Z, ZENG T, DING J. Reverse engineering approach to focus shaping[J]. Optics Letters, 2016, 41(9): 1929-1932. doi: 10.1364/OL.41.001929 [2] CHEN R P, CHEN Z, GAO Y, et al. Flexible manipulation of the polarization conversions in a structured vector field in free space[J]. Laser & Photonics Reviews, 2017, 11(6): 1700165. [3] LIU Z Y, LI L, HU B T. Focusing property for ultra-short pulse laser reflected by off-axis parabolic mirrors[J]. Laser Technology, 2012, 36(5): 657-661(in Chinese). [4] ZHAO J H, WANG Q, ZHU B W, et al. Compact focusing properties of radial vector beam with vortex phase encoding[J]. Laser Technology, 2017, 41(2): 187-190(in Chinese). [5] ZHAN Q. Trapping metallic Rayleigh particles with radial polarization[J]. Optics Express, 2004, 12(15): 3377-3382. doi: 10.1364/OPEX.12.003377 [6] KOZAWA Y, SATO S. Optical trapping of micrometer-sized dielectric particles by cylindrical vector beams[J]. Optics Express, 2010, 18(10): 10828-10833. doi: 10.1364/OE.18.010828 [7] ZHAO Y, ZHAN Q, ZHANG Y, et al. Creation of a three-dimensional optical chain for controllable particle delivery[J]. Optics Le-tters, 2005, 30(8): 848-850. doi: 10.1364/OL.30.000848 [8] VENKATAKRISHNAN K, TAN B. Interconnect microvia drilling with a radially polarized laser beam[J]. Journal of Micromechanics and Microengineering, 2006, 16(12): 2603-2607. doi: 10.1088/0960-1317/16/12/013 [9] KRAUS M, AHMED M A, MICHALOWSKI A, et al. Microdrilling in steel using ultrashort pulsed laser beams with radial and azimuthal polarization[J]. Optics Express, 2010, 18(21): 22305-22313. doi: 10.1364/OE.18.022305 [10] LAN T H, TIEN C H. Servo study of radially polarized beam in high numerical aperture optical data storage system[J]. Japanese Journal of Applied Physics, 2007, 46(6s): 3758-3760. [11] KIM W C, PARK N C, YOON Y J, et al. Investigation of near-field imaging characteristics of radial polarization for application to optical data storage[J]. Optical Review, 2007, 14(4): 236-242. doi: 10.1007/s10043-007-0236-5 [12] YUAN G H, WEI S B, YUAN X C. Nondiffracting transversally polarized beam[J]. Optics Letters, 2011, 36(17): 3479-3481. doi: 10.1364/OL.36.003479 [13] ZHANG M M, BAI Sh Ch, DONG J. Advances in Ince-Gaussian modes laser[J]. Laser & Optoelectronics Progress, 2016, 53(2): 020002(in Chinese). [14] BANDRES M A, GUTIÉRREZ-VEGA J C. Ince-Gaussian beams[J]. Optics Letters, 2004, 29(2): 144-146. [15] BANDRES M A. Elegant Ince-Gaussian beams[J]. Optics Letters, 2004, 29(15): 1724-1726. doi: 10.1364/OL.29.001724 [16] BANDRES M A, GUTIÉRREZ-VEGA J C. Ince-Gaussian modes of the paraxial wave equation and stable resonators[J]. Journal of The Optical Society of America, 2004, A21(5): 873-880. [17] WOERDEMANN M, ALPMANN C, DENZ C. Optical assembly of microparticles into highly ordered structures using Ince-Gaussian beams[J]. Applied Physics Letters, 2011, 98(11): 111101. doi: 10.1063/1.3561770 [18] WOERDEMANN M, ALPMANN C, ESSELING M, et al. Advanced optical trapping by complex beam shaping[J]. Laser & Photonics Reviews, 2013, 7(6): 839-854. [19] GATHER M C, YUN S H. Single-cell biological lasers[J]. Nature Photonics, 2011, 5(7): 406-410. doi: 10.1038/nphoton.2011.99 [20] PLICK W N, KRENN M, FICKLER R, et al. Quantum orbital angular momentum of elliptically symmetric light[J]. Physical Review, 2013, A87(3): 033806. [21] KRENN M, FICKLER R, HUBER M, et al. Entangled singularity patterns of photons in Ince-Gauss modes[J]. Physical Review, 2013, A87(1): 012326. [22] OTTE E, DENZ C. Sculpting complex polarization singularity networks[J]. Optics Letters, 2018, 43(23): 5821-5824. [23] OTTE E, ASCHÉ E, DENZ C. Shaping optical spin flow topologies by the translation of tailored orbital phase flow[J]. Journal of Optics, 2019, 21(6): 064001. [24] HAN W, YANG Y, CHENG W, et al. Vectorial optical field generator for the creation of arbitrarily complex fields[J]. Optics Express, 2013, 21(18): 20692-20706. [25] RICHARDS B, WOLF E. Electromagnetic diffraction in optical systems, Ⅱ. Structure of the image field in an aplanatic system[J]. Proceedings of The Royal Society, 1959, A253(1274): 358-379. [26] ZHAN Q. Cylindrical vector beams: From mathematical concepts to applications[J]. Advances in Optics and Photonics, 2009, 1(1): 1-57. -
点击查看大图
图(8)
计量
- 文章访问数: 12790
- HTML全文浏览量: 8289
- PDF下载量: 61
- 被引次数: 0
