网站地图
下载:
-
低空风切变指的是在距地面600m范围内，风矢量(风速、风向)在水平或垂直距离上发生明显改变的现象[1]，具有时间短、类型多变、破坏力强等特点，且常伴随着有极端天气产生，为飞行器的起飞和降落带来了极大的困扰[2]。根据国际民航组织(International Civil Organization, ICAO)的规定：风切变强度分为轻度、中度、重度、严重4个等级，可用风切变因子来表示。风切变因子是指空间两点距离(水平距离或垂直距离)为30m时风矢量差的大小[3]。由于大部分飞行事故都发生在飞机起飞和进近阶段，因此，机场的风场探测技术尤为重要。相干激光测风雷达作为一种新型的探测装置，体积小、重量轻、抗干扰能力强、分辨率高，能够弥补其它探测手段的不足，尤其是在晴空条件下最有效的风场探测手段，对保障飞机起降安全、预警低空风切变有重要指导作用，因此，利用激光测风雷达，准确地对低空风场预测是保证飞行的重要工具。
20世纪70年代，著名气象学家FUJITA在调查了3次飞机飞行事故后，认为始作俑者为强烈的下沉气流，从此开启风切变的研究[4]。1983年，WOODFIELD和WOODS提出的S因子算法[5]，在某些特殊情况下仅通过最大最小值之间的差值会产生较大误差。2011年，香港天文台CHEN等人提出香港机场沿用至今的单斜坡低空风切变自动预警算法[6]和一种新的下滑道扫描策略[7]，但是该算法由于受到斜坡长度的限制仅对小尺度风切变有更好的效果。2012年，CHEN提出F因子算法[8]，但直接计算由激光雷达得到的逆风梯度数据可能会导致快速波动且无法计算垂直分量的风切变。2014年，他们又提出利用涡流耗散率[9]预警低空风切变，但因为涡流耗散率的阈值在国际中没有明确的规定，该方法还需要在实际应用中继续探索。2016年，JIANG等人提出单双斜坡结合的算法[10]来预警风切变，不足的是该算法只能预警大尺度风切变。2019年，MA等人提出基于主成分分析(principal component analysis, PCA)和相位差校正法的风切变预警算法[11]，但是该算法存在一定的问题且结果不够准确，多普勒频移和风切变阈值还需要进一步通过经验确定。
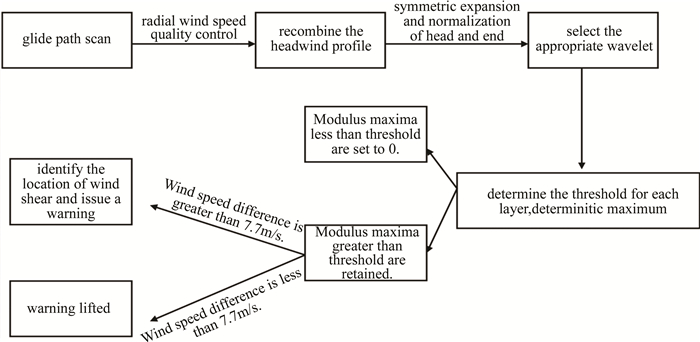
鉴于现有算法存在不足，本文中提出了一种基于小波变换模极大值的激光雷达风切变预警算法。该算法通过选取一定的小波函数确定重组逆风廓线上的模极大值，再根据模极大值的阈值确定是否有风切变发生，最终确定风切变发生的位置和时刻。
-
通过检测小波变换模极大值来检测信号奇异点的方法最早是由MALLAT等人提出[12]，后人对此加以引申并应用到了电力系统故障检测[13]、心电图异常信号检测[14-15]、桥梁裂缝检测[16]。在风切变的检测中，风切变可以看成是径向速度信号的突变信号。信号发生的突变时刻被认为是信号的奇异点，而小波变换模极大值通常正好对应着信号的突变点，因此，基于小波变换模极大值检测方法可用于低空风切变预警，通过检测速度径向数据的小波变换模极大值确定信号的突变位置，即检测飞机下滑道上风切变发生的时刻和位置。
MALLAT系统地论述了如何利用小波变换的局部化特性检测信号奇异点位置[12]，并对小波变换的定义采用了具有滤波意义的卷积形式[17]。
设ψ(x)为一个小波母函数，满足容许性条件，尺度为a的小波母函数为$ \psi_a(x)=\frac{1}{a} \psi\left(\frac{x}{a}\right)$，其小波变换为f(x)和ψa(x)的卷积如(1)式所示，其在物理意义上表现为脉冲响应为ψa(x)的滤波器对信号f(x)的滤波：
$ \begin{gathered} W_\psi(a, x)=f(x) * \psi_a(x)= \\ \frac{1}{a} \int_{-\infty}^{+\infty} f(x) \psi\left(\frac{x-\tau}{a}\right) \mathrm{d} \tau \end{gathered} $
(1) 式中，τ为时间。
设具有低通平滑作用的滤波函数θ(x)满足：$ \int_{-\infty}^{+\infty} \theta(x) \mathrm{d} x=1$和$ \lim\limits _{x \mapsto \rightarrow \infty} \theta(x)=0$，其1阶导数和2阶导数分别用ζ(x)和η(x)表示：
$ \zeta(x)=\frac{\mathrm{d} \theta(x)}{\mathrm{d} x} $
(2) $ \eta(x)=\frac{\mathrm{d}^2 \theta(x)}{\mathrm{d} x} $
(3) 根据Fourier变换的微分性质，ζ(x)，η(x)均满足容许性条件，均可作为小波母函数。对其分别做小波变换，有：
$ \begin{gathered} W_\zeta(a, x)=\frac{1}{a} \int_{-\infty}^{+\infty} f(x) \zeta\left(\frac{x-\tau}{a}\right) \mathrm{d} \tau= \\ a \frac{\mathrm{d}}{\mathrm{d} x}\left[f(x) * \theta_a(x)\right] \end{gathered} $
(4) $ \begin{gathered} W_\eta(a, x)=\frac{1}{a} \int_{-\infty}^{+\infty} f(x) \eta\left(\frac{x-\tau}{a}\right) \mathrm{d} \tau= \\ a^2 \frac{\mathrm{d}^2}{\mathrm{~d} x^2}\left[f(x) * \theta_a(x)\right] \end{gathered} $
(5) 式中，Wζ(a, x)是f(x)通过滤波器θa(x)滤波后的1阶导数。由于θa(x)是一个平滑滤波函数，所以f(x)经过θa(x)滤波后，f(x)的噪声得到了抑制；而1阶导数，即微分运算，反映了f(x)的变化率，当存在突变点时，它的变化率就很大，达到模极大值，所以Wζ(a, x)取极值点的地方就是f(x)的边沿位置。Wη(a, x)是通过滤波器θa(x)滤波后的2阶导数，2阶导数的过零点对应1阶导数的极值点，所以也常用Wη(a, x)的过零点来检测信号的突变点，但是对于受到强噪声污染的信号，Wη(a, x)的过零点很多，由此很难真正的判断信号的边沿。此外，Wη(a, x)的过零点只能给出拐点的位置信息，不能给出变换的快慢，所以本文中用Wζ(a, x)的模极大值来检测径向速度信号的风切变。若对x0的任意邻域内的任意点x有|W(a0, x)|≤|W(a0, x0)|，则称点(a0, x)为小波变换的模极大值。
图 1是本文中提出的新算法的流程图。
Figure 1. Algorithm flow chart
-
首先讨论小波变换阶数及插值对检测结果的影响，由于横坐标表示下滑道上距离飞机降落点的距离，每个点间隔为100m，即0.1km，故插值的步长选为0.05。阶数影响的结果如图 2所示，插值影响的结果如图 3所示。
Figure 2. The normalized results of modulus maxima of different orders
Figure 3. Influence of interpolation on detection results
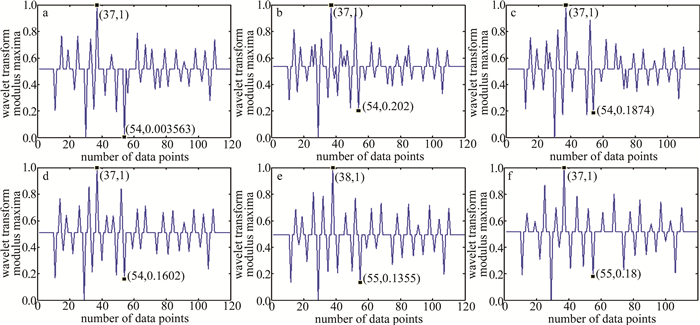
图 2是在不同分解阶数下使用相同小波得到的结果。其中图 2a~图 2f中的阶数依次为1~6。由图 3a可知，最大的两个速度突变点发生在x=38和x=55处，而图 2中只有图 2e即分解阶数为5阶时是准确的。再通过其它数据验算，表明此算法检测激光雷达测量反演得到的重组逆风廓线最适合的分解阶数为5阶，故后面的验证将全部采用5阶小波变换分解。
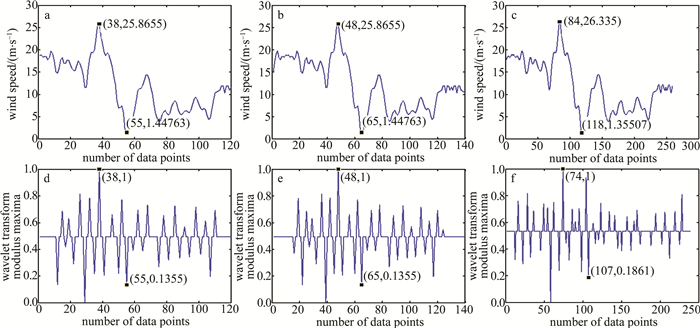
图 3是插值对检测结果的影响。其中图 3a~图 3c分别为原始重组逆风廓线、首尾镜像延长各10个点的重组逆风廓线、先插值再首尾延长各10个点的重组逆风廓线，图 3d~图 3f是分别对图 3a~图 3c做小波变换、求模极大值并归一化的结果。根据图 3的结果，显然，直接处理数据和首尾镜像延长后再处理数据没有区别，而先插值后延长的处理方式使结果有10个数据点左右的偏差，考虑到插值采用的是样条插值，会额外数据个数，即增加了径向速度数据中本不存在的速度值，所以导致了结果的偏移。再验证了其它数据之后可以确定，在对激光雷达测量得到的重组逆风廓线处理时不需要插值。而对于首尾镜像延长的步骤，是有必要的，这一步是为了防止首尾突变的风速信息缺失。经过验证，首尾镜像延长不会对小波变换模极大值的结果造成影响。
-
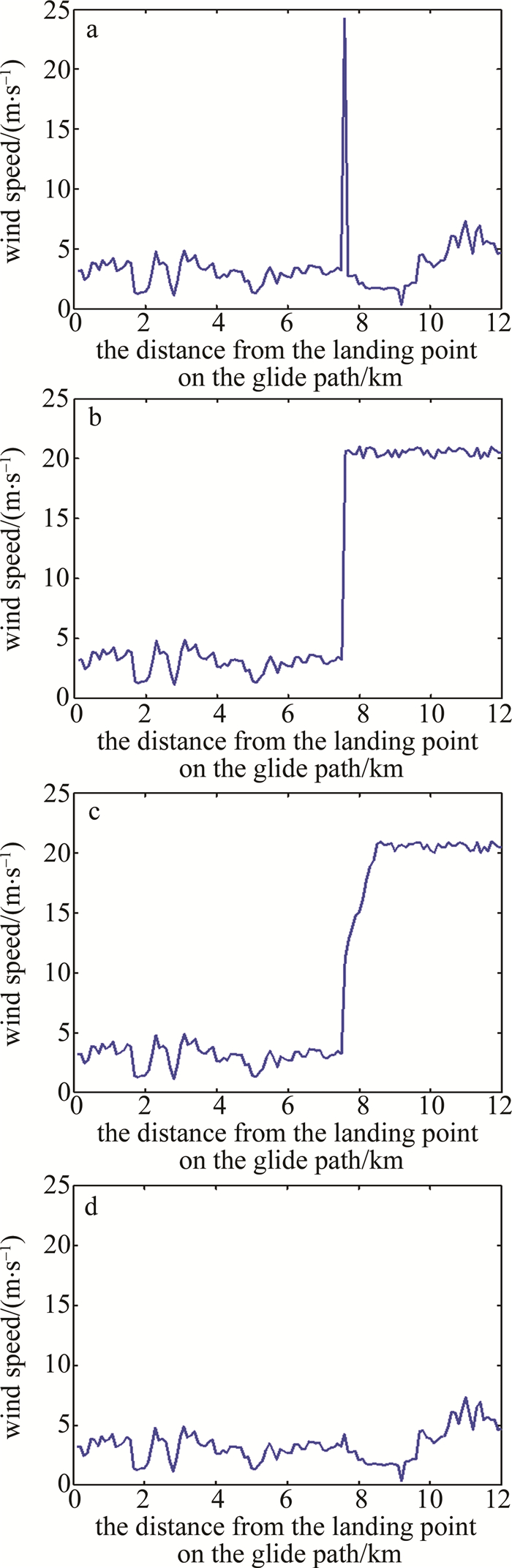
为了验证上述算法的可行性和准确性，首先构造了几组比较有代表性的径向速度数据。数据点数均为120个，数据如图 4所示。其中图 4a为脉冲数据，图 4b为阶跃数据，图 4c为斜坡数据，图 4d为明显未发生风切变数据。4组数据的横坐标表示下滑道上距离飞机降落点的距离，每个点间隔100m；纵坐标表示风速，单位为m/s。突变点均设置在距离下滑道上距离飞机降落点7.6km处，即横坐标x=76。利用以下4组数据分别采用双正交(biorthogonal，Bior)小波、多贝西(Daubechies，Db)小波对算法进行数值验证。
Figure 4. Four groups of reconstructed upwind profiles of the structure
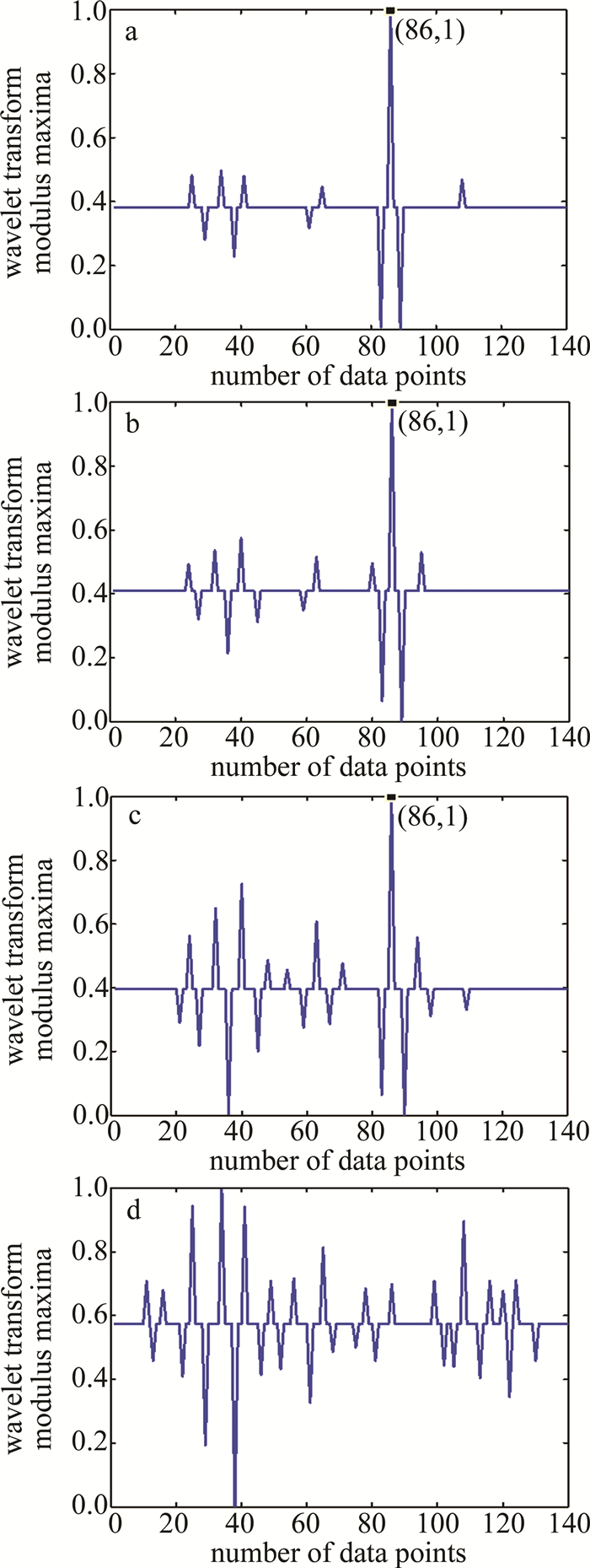
经过大量小波对4组数据的验证，表明脉冲型数据使用Bior系中双数小波检结果较准确；阶跃型和斜坡型数据用Db系中Db5检测结果较准确。在验证过程中数据首尾延长各10个数据点防止信息缺失，由于本文中所说的模极大值实际意义是模的极大值和模的极小值，为了避免出现负值，生成的模极大值结果又经过归一化处理，最终如图 5所示。
Figure 5. Wavelet transform modulus maximum result
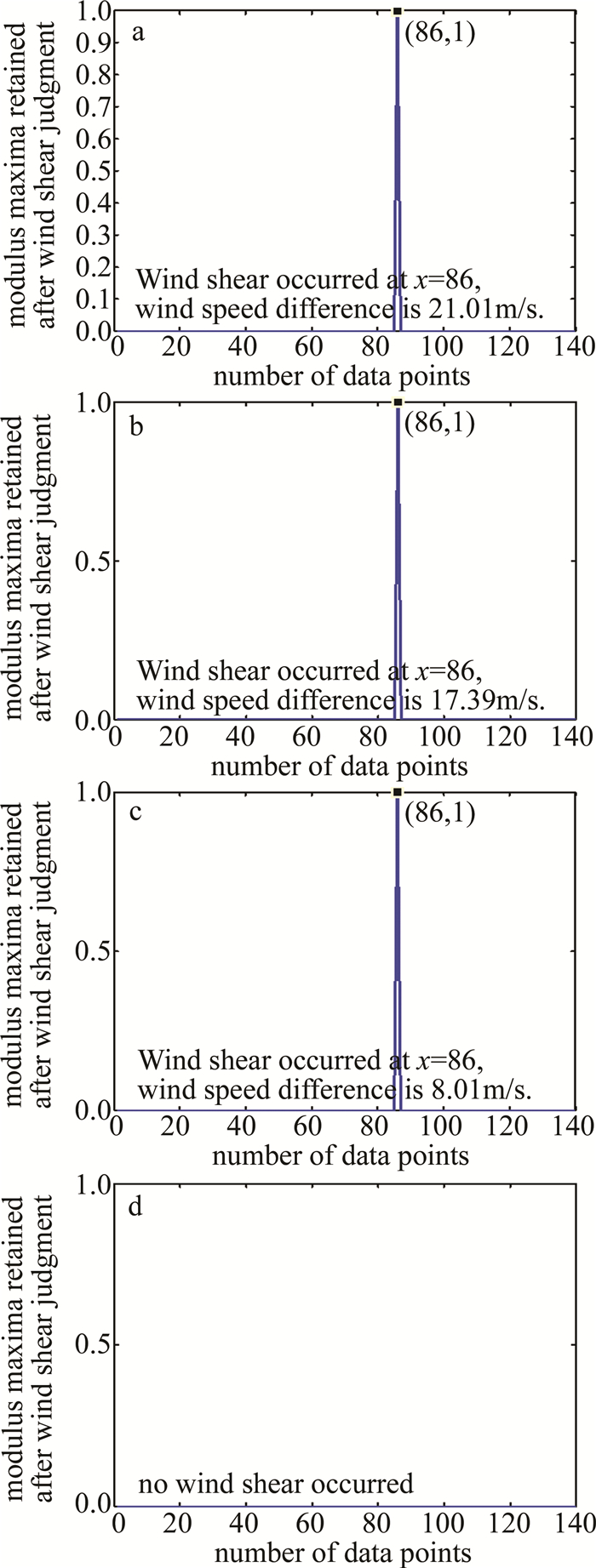
图 6是经过风切变判断后保留的模极大值结果，即为风切变发生的位置。由于图 4中1~3组数据设置的突变点位置均为下滑道上距离飞机降落点7.6km处，即第76个数据点发生突变，数据首端经镜像延长10个数据点后，应在第86个数据点发生突变。图 5展示的都是准确找到了第86个数据点的小波变换模极大值的结果，其中图 5a、图 5d中选取的小波为Bior6.8小波，图 5b、图 5c中选取的小波为Db5小波。经过风切变判断后，图 6a~图 6c中也仅仅只保留了第86个数据点的模极大值，而图 6d中的模极大值全部置为0，预设值的结果完全一致，预警率达到100%。至此，基于小波变换模极大值的激光雷达风切变预警算法在数值验证上通过。
Figure 6. Test result after windshear judgment
-
2017-08-08，鄂西北郧西县马安乡发生了局地大暴雨，使用中国气象局的CINRAD/SA型S波段多普勒雷达对暴雨进行了监测，该雷达一个平面位置显示器(plane position indicator，PPI)扫描周期为6min, 可以测量920个距离库230km范围内的天气情况。结果显示，20:24:00时最大风速为20.1m/s，20:30:06时最大风速为27.5m/s，20:36:13时最大风速降为19m/s，此处粗略判断有风切变发生。
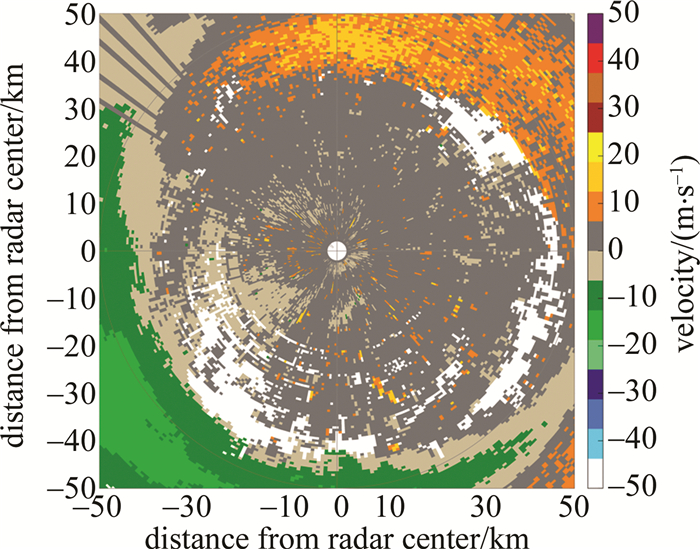
图 7是该时间段内(20:24:00~20:36:13)使用天气雷达测量得到的基本速度。由于直接截取的雷达界面图片较模糊，因此将数据导入MATLAB并重新生成了如图 7所示的基本速度。图 7的看图顺序是从左下角到右上角，图中各颜色色块表示不同的风速和方向，其中白色是速度模糊的部分；左下角浅绿色到深绿色再到中间浅灰色，表明风速是逐渐减小，从-15m/s降到0m/s；右上角由深灰到橙黄色交替，表明风速逐渐增大，最大约为25m/s雷达图的色块反映了有极端强对流导致的风切变发生。
Figure 7. Basic speed measured by weather radar (20:24:00~20:36:13)
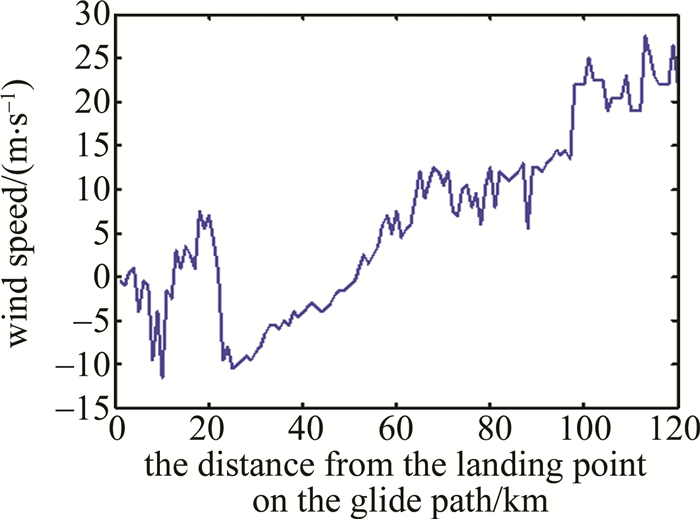
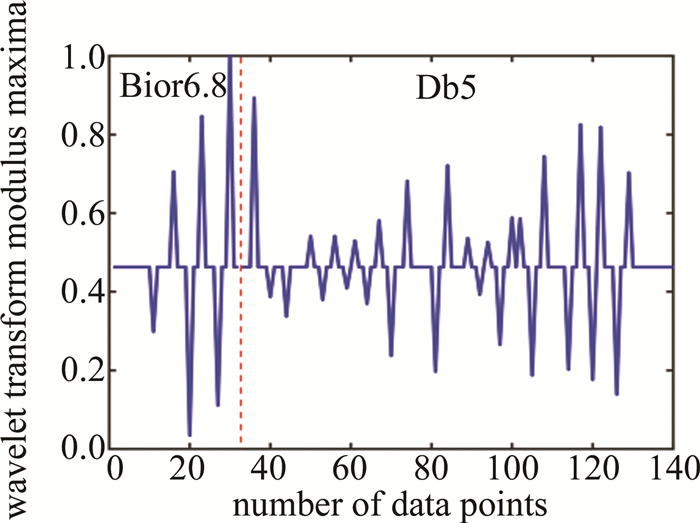
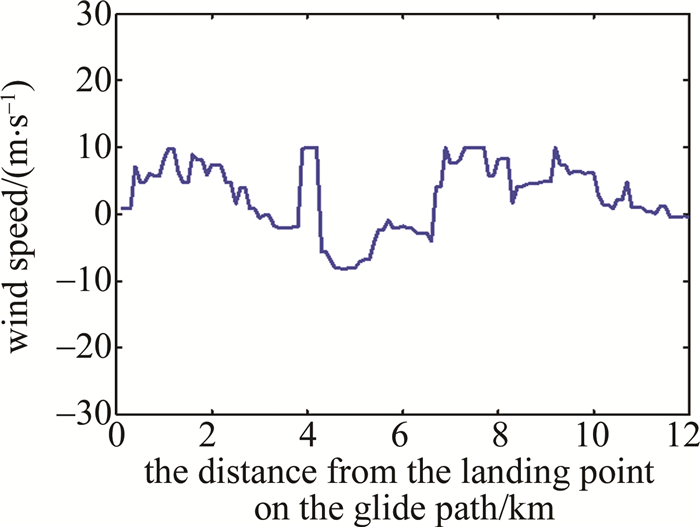
与天气雷达同时测量的激光雷达经数据反演和质量控制后得到如图 8所示的重组逆风廓线，激光雷达仰角为0.5°。由于图 8所示的重组逆风廓线前半段类似脉冲函数(脉冲较宽)，后半段类似斜坡函数，因此根据数值仿真的结果，数据点1~23选取Bior6.8小波，数据点23~120选取Db5小波，分解层数均为5阶，首尾各镜像延长10个数据点，对数据进行处理，得到如图 9所示归一化的模极大值。图 9中前半段为Bior6.8小波处理的模极大值，后半段为Db5小波处理的模极大值，中间为了区分，用红色虚线加以隔开。为了图片的美观，作者将图 9中Db5小波变换模极大值的结果整体平移到与Bior6.8小波变换模极大值的结果在同一水平高度，但是在后续阈值的处理上两部分有不同的阈值。
Figure 8. Reorganization of the headwind profile (20:23:58~20:32:04)
Figure 9. Wavelet transform modulus maximum result
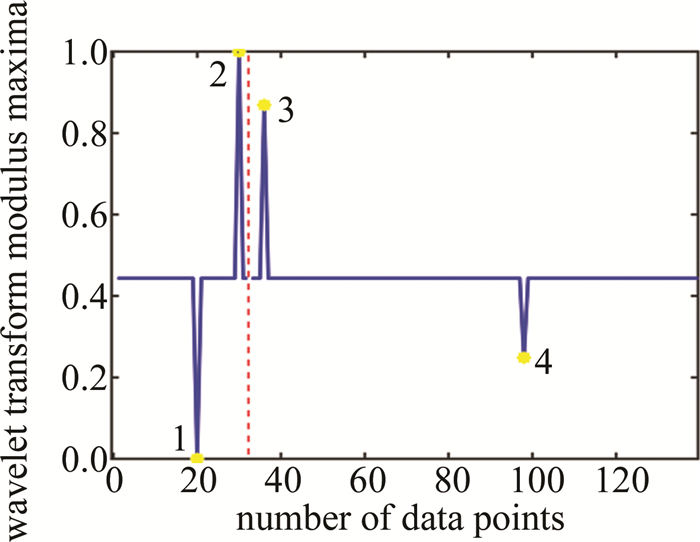
图 10是经过风切变判断后的检测结果。图中，依次在1，2，3，4处有小波变换模极大值保留，由于首端有10个数据点镜像对称延长，且下滑道上每个数据点的距离为0.1km，因此风切变发生的实际位置为下滑道上距离飞机降落点距离1km，2km，2.6km和7.8km处，且风速差依次为-12.5m/s，18.5m/s，17.5m/s和19.5m/s，满足两点间距离超过30m、风速差大于7.7m/s的规定，故确认有风切变发生，风切变强度均为重度。此结果与同时测量的天气雷达和气象局提供的气象资料吻合，证实由于暴雨造成强对流天气，形成风切变，因此基于小波变换模极大值的激光雷达风切变预警算法准确。
Figure 10. Results after windshear judgment
-
2018年3月~11月，在青藏高原东南缘的四川省攀枝花市保安营机场削平的山顶上(经纬度为26°32′32.33″N，101°47′54.67″E)，西南技术物理研究所部署了其研制的3维激光测风雷达来检测机场的风场情况。2018-05-06T13：30，CA4463机组报告“本场五边有颠簸，返航成都”，部署的激光雷达正好进行下滑道扫描[18]，西南技术物理研究所提供了当时的实测下滑道侧向风数据进行分析。重组逆风廓线如图 11所示。
Figure 11. The reconstructed headwind profile measured by 3-D LiDAR (13:22:29~13:31:33)
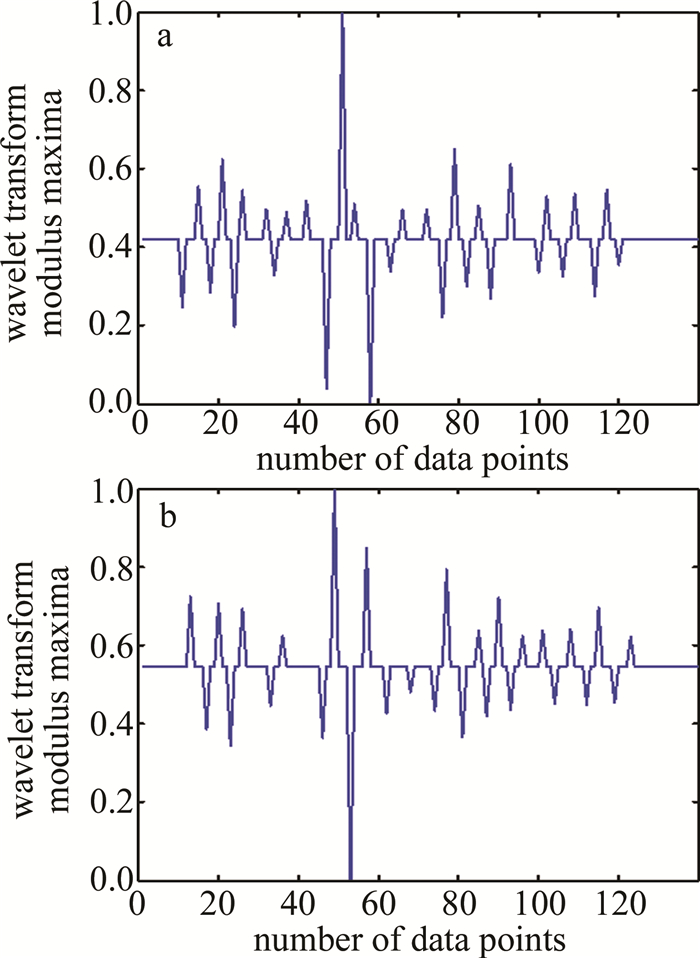
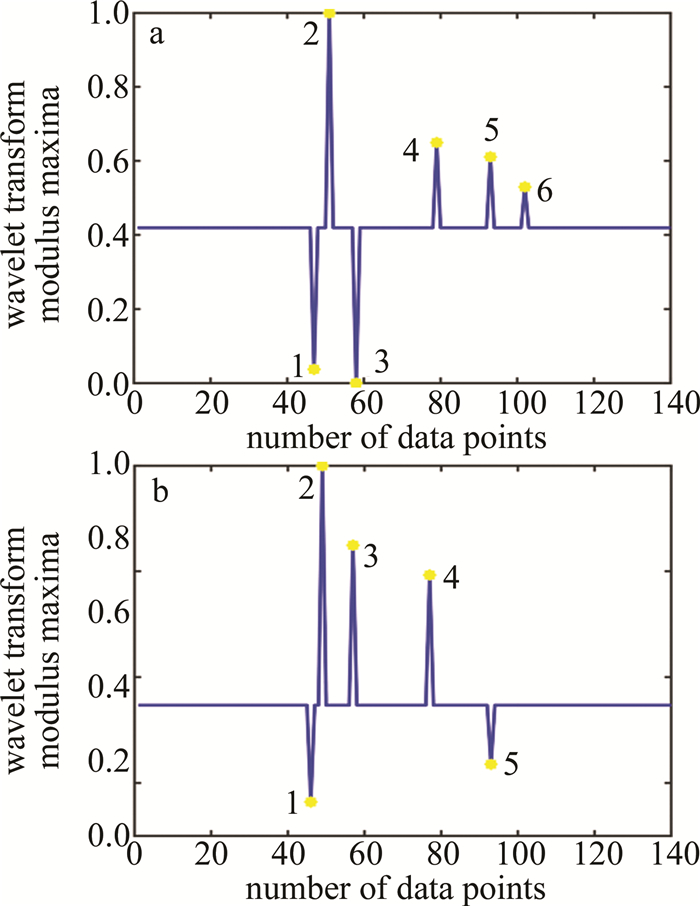
图 12是归一化的小波变换模极大值结果。其中图 12a为Bior6.8小波变换模极大值，图 12b为Db5小波变换模极大值。图 13是经风切变判断后保留的模极大值。其中图 13a是Bior6.8的，图 13b是Db5的。图 12中一些数值较高的模极大值点没有保留，是因为经过风切变判断后，这些奇异点不满足风切变发生的速度差或者距离差，因此被置为0。对比图 13的两幅子图，1、2、3点的结果接近但有1~2个数据点的偏差，且速度差接近；第4个数据点，横坐标(即发生风切变的位置)接近，但风速差差别较大；第5个数据点，两幅子图都是一样的结果；第6个数据点，使用Bior6.8小波时存在，而使用Db5小波时，由于模极大值点在第91个数据点，此时径向风速为4.9m/s，与前后均不满足风速差大于7.7m/s的要求，因此模极大值被置为0，造成最终数据缺失。由于此数据的类型更类似于脉冲型数据，且查阅重组逆风廓线可知, Bior6.8小波的效果较Db5小波更准确。
Figure 12. Wavelet transform modulus maximum result
Figure 13. Test results after windshear judgment
图 13a中，有6个小波变换模极大值保留，同样由于首端有10个数据点镜像对称延长，因此风切变发生的实际位置为下滑道上距离飞机降落点距离3.7km，4.1km，4.8km，6.9km，8.3km和9.2km处，对应的风速差依次为-10.8m/s，11.9m/s，-18.2m/s，14m/s，-8.3m/s和9.2m/s，满足两点间距离超过30m、风速差大于7.7m/s的规定，故确认有风切变发生，风切变强度均为重度。对比西南技术物理研究所的激光雷达判断的风切变和机组的报告，证明基于激光雷达的风切变预警算法是可行的且检测结果准确。
-
本文中提出了一种基于小波变换模极大值的激光雷达低空风切变预警算法。该算法可以检测各种类型的风切变，且不用考虑风切变的产生的原因和风切变的尺度, 同时能够精确检测风切变发生的时刻和位置。通过数值验证和外场测试证实了算法的可行性、准确性和有效性。
基于小波变换模极大值的LiDAR风切变预警算法
Application of LiDAR based on wavelet transform modulus maxima in low-level wind shear alerting
-
摘要: 为了更好地检测低空风切变, 保障飞机的飞行安全, 提出了一种基于小波变换模极大值的激光雷达风切变预警算法。先用小波变换求取重组逆风廓线上的模极大值, 找到"拐点"后再利用风切变判断标准来判断。在进行数值仿真和来自湖北郧西气象站、四川攀枝花机场的现场检测验证后, 确认新算法在准确性及效率方面都有良好的性能, 且脉冲型数据使用biorthogonal系中双数小波检测结果较准确, 而阶跃型和斜坡型数据需使用Daubechies系中Db5小波。结果表明, 鄂西北郧西县和攀枝花保安营机场均有风切变发生, 风切变强度为重度。该算法能检测不同类型的风切变, 不用考虑风切变的尺度, 较好地弥补了现有算法的不足, 为飞机的起降提供技术保障, 对实时检测和预警也有重大的意义。Abstract: For better detection of low-level wind shear, a new algorithm based on the wavelet transform modulus maxima methodI was introduced to predict the occurrence of wind shear along the glide path. Wavelet transform is used to obtain the modulus maximum value on the recombined upwind profile. The "inflection point" was found, and then the windshear judgment standard was used to judge its accuracy. Numerical examples and field detection data from Yunxi Meteorological Station in Hubei Province and Panzhihua Airport in Sichuan Province have well verified the good performance of the method, in terms of both accuracy and efficiency. The result shows that the pulse-type data is more accurate using the even number wavelet in the biorthogonal system; the step-type and ramp-type data is more accurate using the Db5 in the Daubechies system. The results show that the wind shear occurred in Yunxi county and Panzhihua Baoanying Airport, the wind shear intensity were both heavy. This algorithm can detect different types of wind shear without considering the scale of wind shear, which makes up for the shortcomings of existing algorithms, provides technical support for aircraft takeoff and landing, and has great significance for real-time detection and early warning.
-
Figure 11. The reconstructed headwind profile measured by 3-D LiDAR (13:22:29~13:31:33)
-
[1] HUANG T J, TIAN Y H, LI J, et al. Salient region detection and segmentation for general object recognition and image understanding[J]. Science China Information Sciences, 2011, 54(12): 2461-2470. doi: 10.1007/s11432-011-4487-1 [2] ZHANG T, LI Q, ZHENG J F, et al. A study on low-level wind shear caused by microburst using lidar and other data[J]. Laser Technology, 2020, 44(5): 563-569 (in Chinese). [3] INTERNATIONAL CIVIL AVIATION ORGANIZATION. Manual on low-level wind shear[M]. Montreal, Canada: ICAO Headquarters, 2005: 127. [4] FUJITA T T, CARACENA F. An analysis of three weather-related aircraft accidents[J]. Bulletin of American Meteorological Society, 1977, 58(11): 1164-1181. doi: 10.1175/1520-0477(1977)058<1164:AAOTWR>2.0.CO;2 [5] WOODFIELD A A, WOODS J F. Worldwide experience of wind shear during 1981~1982[EB/OL]. (2012-04-24)[2012-12-20]. https://kns-cnki-net-s.nudtproxy.yitlink.com/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD2012&filename=JGHW201212003&uniplatform=NZKPT&v=iXeUOKtQ33zymOZ6%25mmd2Frl6YHL6SCOvg%25mmd2BrNBO1TjIe15psob5o9AYmVkT3ZgFBgkPza. [6] CHAN P W, HON K K, SHIN D K. Combined use of headwind ramps and gradients based on LiDAR data in the alerting of low-level windshear/turbulence[J]. Meteorologische Zeitschrift, 2011, 20(6): 661-670. doi: 10.1127/0941-2948/2011/0242 [7] SHUN C M, CHAN P W. Application of an infrared Doppler lidar in detection of wind shear[J]. Journal of Applied Meteorology and Climatology, 2008, 25(5): 637-655. [8] CHAN P W. Application of LIDAR-based F-factor in windshear alerting[J]. Meteorologische Zeitschrift, 2012, 21(2): 193-204. doi: 10.1127/0941-2948/2012/0321 [9] HON K K, CHAN P W. Application of LiDAR-derived eddy dissipation rate profiles in low-level wind shear and turbulence alerts at Hong Kong International Airport[J]. Royal Meteorological Society, 2013, 21(1): 75-84. [10] JIANG L H, YAN Y, XIONG X L, et al. Doppler LiDAR alerting algorithm of low-level wind shear based on ramps detection[J]. Infrared and Laser Engineering, 2016, 45(1): 0106001(in Chin-ese). doi: 10.3788/irla201645.0106001 [11] MA Y Zh, CHEN N, XIONG X L. Wind shear warning algorithm based on PCA and phase difference correction [J]. Systems Engineering and Electronics, 2019, 42(1): 52-60 (in Chinese). [12] MALLAT S, HWANG W L. Singularity detection and processing with wavelets[J]. IEEE Transactions on Information Theory, 1992, 38(2): 617-643. doi: 10.1109/18.119727 [13] WANG Y, YIN X, XU W, et al. Fault line selection in cooperation with multi-mode grounding control for the floating nuclear power plant grid[J]. Protection and Control of Modern Power Systems, 2020, 16(5): 1-10. [14] CVETKOVIC D, VBEYLI E D, COSIC I. Wavelet transform feature extraction from human PPG, ECG, and EEG signal responses to ELF PEMF exposures: A pilot study [J]. Digital Signal Processing, 2008, 18(5): 861-874. doi: 10.1016/j.dsp.2007.05.009 [15] CHABCHOU S, MANSOURI S, SALAH R B. Impedance cardiography signal denoising using discrete wavelet transform[J]. Australasian Physical and Engineering Sciences in Medicine, 2016, 39: 655-663. doi: 10.1007/s13246-016-0460-z [16] GENTILE A, MESSINA A. On the continuous wavelet transforms applied to discrete vibrational data for detecting open cracks in da-maged beams[J]. International Journal of Solids and Structures, 2003, 40(2): 295-315. doi: 10.1016/S0020-7683(02)00548-6 [17] MALLAT S, HWANG W L. Singularity detection and processing with wavelets[J]. IEEE Transactions on Information Theory, 1992, 38(2): 617-643. doi: 10.1109/18.119727 [18] FENG L T, ZHOU J, FAN Q, et al. Three-dimensional lidar for wind shera detection and early warning in civil aviation airport[J]. Acta Photonica Sinica, 2019, 48(5): 0512001 (in Chinese). doi: 10.3788/gzxb20194805.0512001 -
点击查看大图
图(13)
计量
- 文章访问数: 4267
- HTML全文浏览量: 2912
- PDF下载量: 25
- 被引次数: 0
